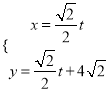题目内容
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(Ⅱ)![]()
![]() 时,讨论
时,讨论![]() 的单调性;进一步地,若对任意的
的单调性;进一步地,若对任意的![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)极小值为![]() ,无极大值;(Ⅱ)答案见解析.
,无极大值;(Ⅱ)答案见解析.
【解析】试题分析:
(Ⅰ)函数的定义域为![]() .
.![]() ,利用导函数研究函数的单调性可得:函数
,利用导函数研究函数的单调性可得:函数![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(Ⅱ)对函数求导![]() ,令
,令![]() ,得
,得![]() ,
, ![]() ,
,
分类讨论可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)函数![]() 的定义域为
的定义域为![]() .
.![]() ,
,
令![]() ,得
,得![]() ;
; ![]() (舍去).
(舍去).
当![]() 变化时,
变化时, ![]() 的取值情况如下:
的取值情况如下:
|
|
|
|
| — | 0 |
|
| 减 | 极小值 | 增 |
所以,函数![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
(Ⅱ)![]() ,
,
令![]() ,得
,得![]() ,
, ![]() ,
,
当![]() 时,在区间
时,在区间![]() ,
, ![]() 上,
上, ![]() ,
,![]() 单调递减,
单调递减,
在区间![]() 上,
上, ![]() ,
,![]() 单调递增.
单调递增.
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 单调递减;
单调递减;
所以,当![]() 时,
时, ![]() ,
, ![]()
![]()
即![]() ,
,
因为, ![]() ,所以,实数
,所以,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 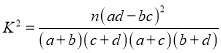 )
)