题目内容
12.某品牌乒乓球按质量标准分为1,2,3,4四个等级,现从某工厂生产的一批乒乓球中随机抽取20个,对其等级进行统计分析,得到的频率分布表如下:| 等级 | 1 | 2 | 3 | 4 |
| 频率 | m | n | 0.5 | 0.2 |
(Ⅱ)在(Ⅰ)的条件下,从等级为1和2的乒乓球中任意抽取2个,求抽取的2个乒乓球等级相同的概率.
分析 (Ⅰ)通过频率分布表得推出m+n=0.3.利用等级系数为1的恰有2件,求出m,然后求出n.
(Ⅱ)根据条件列出满足条件所有的基本事件总数,“从x1,x2,y1,y2,y3,y4这6件日用品中任取两件,等级系数相等”的事件数,求解即可.
解答 解:(Ⅰ)由频率分布表得 m+n+0.5+0.2=1,
即 m+n=0.3.…(2分)
由抽取的20个零件中,等级为1的恰有2个,
得 m=$\frac{2}{20}$=0.1.…(4分)
所以n=0.3-0.1=0.2.…(5分)
(Ⅱ):由(Ⅰ)得,等级为1的零件有2个,记作x1,x2,
等级为2的零件有4个,记作y1,y2,y3,y4,
从x1,x2,x3,y1,y2,y3,y4中任意抽取2个零件,
所有可能的结果为:
(x1,x2),(x1,y1),(x1,y2),(x1,y3),(x1,y4),
(x2,y1),(x2,y2),(x2,y3),(x2,y4),(y1,y2),
(y1,y3),(y1,y4),(y2,y3),(y2,y4),(y3,y4),
共计15种.…(9分)
记事件A为“从零件x1,x2,y1,y2,y3,y4中任取2件,其等级相等”.
则A包含的基本事件为(x1,x2),(y1,y2),(y1,y3),(y1,y4),(y2,y3),(y2,y4),(y3,y4)共7个.…(11分)
故所求概率为 P(A)=$\frac{7}{15}$.…(12分)
点评 本题考查概率、统计等基本知识,考查数据处理能力、运算能力、应用意识.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2.设随机变量ξ服从正态分布N(2,σ2),若P(ξ>4)=0.1,则P(ξ<0)=( )
| A. | 0.4 | B. | 0.2 | C. | 0.1 | D. | 0.05 |
7.已知一扇形的圆心角的弧度数为2,其弧长也是2,则该扇形的面积为( )
| A. | 1 | B. | 2 | C. | sin1 | D. | 2sin1 |
1.已知a是实数,则$\frac{1}{a}$<1是a>1的( )
| A. | 既不充分又不必要条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 必要不充分条件 |
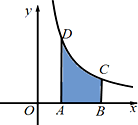 如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数)
如图,曲边梯形ABCD由直线x=1,x=e,x轴及曲线y=$\frac{3}{x}$围成,则这个曲边梯形的面积是3.(注:e为自然对数的底数)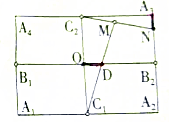 如图,O是矩形A1A2A3A4的中心,B1,B2,C1,C2分别是矩形四条边的中点,A1A2=4,A2A3=2$\sqrt{3}$,若以B1B2所在直线为x轴,O为坐标原点建立平面直角坐标系,记以O为对称中心,同时经过点C2,B2的椭圆为W.
如图,O是矩形A1A2A3A4的中心,B1,B2,C1,C2分别是矩形四条边的中点,A1A2=4,A2A3=2$\sqrt{3}$,若以B1B2所在直线为x轴,O为坐标原点建立平面直角坐标系,记以O为对称中心,同时经过点C2,B2的椭圆为W.