题目内容
20.已知由y=x2+4ax-4a+3,y=x2+(a-1)x+a2,y=x2+2ax-2a确定的三条抛物线中至少有一条与x轴有交点,求实数a的取值范围.分析 假设三条抛物线都不与x轴有交点,则y=x2+4ax-4a+3,y=x2+(a-1)x+a2,y=x2+2ax-2a的判别式均小于0,进而求出相应的实数a的取值范围,进而根据这与已知相对立,得到答案.
解答 解:假设三条抛物线都不与x轴有交点,…..(3分)
设y=x2+4ax-4a+3,y=x2+(a-1)x+a2,y=x2+2ax-2a的判别式分别为:△1,△2,△3,
则$\left\{\begin{array}{l}{△}_{1}=(4{a)}^{2}-4(-4a+3)<0\\{△}_{1}=({a-1)}^{2}-4{a}^{2}<0\\{△}_{1}=(2{a)}^{2}-4(-2a)<0\end{array}\right.$.….(8分)
即$\left\{\begin{array}{l}-\frac{3}{2}<a<\frac{1}{2}\\ a<-1,或a>\frac{1}{3}\\-2<a<0\end{array}\right.$,
解得:$-\frac{3}{2}<a<-1$,…(10分)
又由y=x2+4ax-4a+3,y=x2+(a-1)x+a2,y=x2+2ax-2a确定的三条抛物线中至少有一条与x轴有交点,
则$a≤-\frac{3}{2},或a≥-1$…..(12分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键,难度不大,属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
10.已知x∈[0,π],则函数y=$\sqrt{3}$sinx-cosx的值域为( )
| A. | [-2,2] | B. | [-1,2] | C. | [-1,1] | D. | [0,2] |
12.某品牌乒乓球按质量标准分为1,2,3,4四个等级,现从某工厂生产的一批乒乓球中随机抽取20个,对其等级进行统计分析,得到的频率分布表如下:
(Ⅰ)在抽取的20个乒乓球中,等级为1的恰有2个,求m,n的值;
(Ⅱ)在(Ⅰ)的条件下,从等级为1和2的乒乓球中任意抽取2个,求抽取的2个乒乓球等级相同的概率.
| 等级 | 1 | 2 | 3 | 4 |
| 频率 | m | n | 0.5 | 0.2 |
(Ⅱ)在(Ⅰ)的条件下,从等级为1和2的乒乓球中任意抽取2个,求抽取的2个乒乓球等级相同的概率.
9.三位男生和一位女生并排照相,若女生不排在两端,则不同的排法共有( )
| A. | 6种 | B. | 12种 | C. | 18种 | D. | 24种 |
6.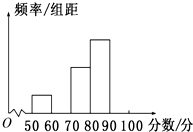 为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)不具体计算频率/组距,补全频率分布直方图.
 为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| [50,60) | 4 | 0.08 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.20 |
| [80,90) | 16 | 0.32 |
| [90,100] | ||
| 合计 |
(2)不具体计算频率/组距,补全频率分布直方图.
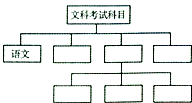 安徽省2015年高考文科考试科目有语文、数学、英语和文综,文综是指政治、历史、地理等三科合在一张卷子上,请你将图补充完整.
安徽省2015年高考文科考试科目有语文、数学、英语和文综,文综是指政治、历史、地理等三科合在一张卷子上,请你将图补充完整.