题目内容

2．设随机变量ξ服从正态分布N（2，σ2），若P（ξ＞4）=0.1，则P（ξ＜0）=（　　）
A．0.4B．0.2C．0.1D．0.05

分析 随机变量ξ服从正态分布N（2，σ2），得到曲线关于x=2对称，根据曲线的对称性得到P（ξ＜0）=P（ξ＞4），从而得到所求

解答 解：随机变量ξ服从正态分布N（2，σ2），
∴曲线关于x=2对称，
∴P（ξ＜0）=P（ξ＞4）=0.1，
故选：C．

点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查概率的性质，是一个基础题．

练习册系列答案
相关题目
12．某研究结构对高中学段学生的记忆能力x和识图能力y进行统计分析，得到如下数据：
x0123
y-11m8
若y与x的回归直线方程$\widehat{y}$=3x-$\frac{3}{2}$，则实数m的值是4．
13．已知椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{4}$=1（a＞2），F1、F2为椭圆的左、右焦点，A、B为椭圆的左、右顶点，点P为椭圆上异于A、B的动点，且直线PA、PB的斜率之积为-$\frac{1}{2}$．
（1）求椭圆的方程；
（2）若动直线l与椭圆有且仅有一个公共点，求证：点F1、F2到直线l的距离乘积为定值．
10．已知x∈[0，π]，则函数y=$\sqrt{3}$sinx-cosx的值域为（　　）
A．[-2，2]B．[-1，2]C．[-1，1]D．[0，2]
17．已知|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，且向量$\overrightarrow{a}$与$\overrightarrow{b}$互相垂直．
（Ⅰ）若向量$\overrightarrow{c}$=3k$\overrightarrow{a}$+4k$\overrightarrow{b}$（k∈R），且|$\overrightarrow{c}$|=12$\sqrt{2}$，求|k|的值；
（Ⅱ）若向量$\overrightarrow{c}$满足（$\overrightarrow{a}-\overrightarrow{c}$）$⊥（\overrightarrow{c}-\overrightarrow{b}）$，求|$\overrightarrow{c}$|的取值范围．
7．一元二次不等式x2-5x-6＜0的解集为（-1，6）．
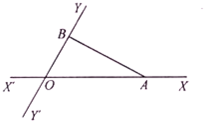14．如图，有两条相交成60°角的直路XX′，YY′，交点是O，甲和乙同时从点O出发，甲沿着OX的方向，乙沿着OY的方向，经过若干小时后，甲到达点A，乙到达点B，此时甲测得他走过的路程比他到乙的距离多2km，且乙走过的路程超过4km，设甲到达点A，乙到达点B时，乙走过的路程为x km，甲走过的路程为y km．
（1）求甲走过的路程y km与乙走过的路程x km的函数关系式；
（2）设甲到达点A，乙到达点B时，两人走过的路程之和为S km，求S的最小值．
11．甲、乙两人下棋，结果是一人获胜或下成和棋，已知甲不输的概率为0.6，乙不输的概率为0.7，则两人下成和棋的概率为0.3．
12．某品牌乒乓球按质量标准分为1，2，3，4四个等级，现从某工厂生产的一批乒乓球中随机抽取20个，对其等级进行统计分析，得到的频率分布表如下：
等级1234
频率mn0.50.2
（Ⅰ）在抽取的20个乒乓球中，等级为1的恰有2个，求m，n的值；
（Ⅱ）在（Ⅰ）的条件下，从等级为1和2的乒乓球中任意抽取2个，求抽取的2个乒乓球等级相同的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网