Question

【题目】(2017·合肥市质检)已知点F为椭圆E： (a>b>0)的左焦点，且两焦点与短轴的一个顶点构成一个等边三角形，直线与椭圆E有且仅有一个交点M.

(1)求椭圆E的方程；

(2)设直线与y轴交于P，过点P的直线l与椭圆E交于不同的两点A，B，若λ|PM|2＝|PA|·|PB|，求实数λ的取值范围．

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）由两焦点与短轴的一个顶点构成一个等边三角形，直线与椭圆有且仅有一个交点可得关于， 的方程组，求出， 的值，即可得到椭圆的方程；（2）由（1）求得坐标，得到的值，当直线与轴垂直时，直接由，求得值；当直线与轴不垂直时，设直线的方程为，联立直线方程与椭圆方程，利用判别式大于求得的取值范围，再由根与系数的关系，结合，把用含有的表达式表示，则实数的取值范围可求.

试题解析：(1)由题意，得a＝2c，b＝c，则椭圆E为.

由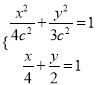，得x2－2x＋4－3c2＝0.

∵直线与椭圆E有且仅有一个交点M，

∴Δ＝4－4(4－3c2)＝0c2＝1，

∴椭圆E的方程为.

(2)由(1)得M，

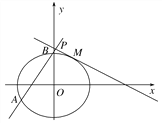
∵直线与y轴交于P(0,2)，

∴|PM|2＝，

当直线l与x轴垂直时，

|PA|·|PB|＝(2＋)×(2－)＝1，

∴λ|PM|2＝|PA|·|PB|λ＝，

当直线l与x轴不垂直时，设直线l的方程为y＝kx＋2，A(x1，y1)，B(x2，y2)，

由(3＋4k2)x2＋16kx＋4＝0，

依题意得，x1x2＝，且Δ＝48(4k2－1)>0，

∴|PA|·|PB|＝(1＋k2)x1x2＝(1＋k2)·＝1＋＝λ，

∴λ＝ (1＋)，

∵k2>，∴<λ<1.

综上所述，λ的取值范围是[，1)．