题目内容
【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员x名.
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求x的值;
(Ⅱ)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择,求该客户最终聘请的家政服务员中既有A类又有B类的概率.
【答案】(Ⅰ) x=48(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)由分层抽样的性质列出方程,求出![]() .
.
(Ⅱ)基本事件总数![]() 该客户最终聘请的家政服务员中既有A类又有B类包含的基本事件个数
该客户最终聘请的家政服务员中既有A类又有B类包含的基本事件个数![]() 由此能求出该客户最终聘请的家政服务员中既有A类又有B类的概率.
由此能求出该客户最终聘请的家政服务员中既有A类又有B类的概率.
试题解析:(Ⅰ)20-16=4,由![]() x=16,可得x=48
x=16,可得x=48
(Ⅱ)设3名A类家政服务员的编号为a,b,c,2名B类家政服务员的编号为1,2,
则所有可能情况有:(a,b),(a,c),(a,1),(a,2),(b,c),(b,1),(b,2),(c,1),(c,2),(1,2)共10种选择.
该客户最终聘请的家政服务员中既有A类又有B类的情况有:
(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)共6种选择,
∴该客户最终聘请的家政服务员中既有A类又有B类的概率为
P=![]() =
=![]() .
.

【题目】已知函数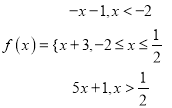
(1)求函数f(x)的最小值;
(2)已知m∈R,p:关于x的不等式f(x)≥m2+2m-2对任意x∈R恒成立,q:函数y=(m2-1)x是增函数,若p正确,q错误,求实数m的取值范围.
【题目】某种产品按质量标准分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
等级 |
|
|
|
|
|
频率 |
|
|
|
|
|
(1)在抽取的20个产品中,等级为5的恰有2个,求![]() ,
,![]() ;
;
(2)在(1)的条件下,从等级为3和5的所有产品中,任意抽取2个,求抽取的2个产品等级恰好相同的概率.