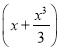Question

【题目】已知函数f(x)＝x2＋b图象上的点P(2,1)关于直线y＝x的对称点Q在函数g(x)＝lnx＋a上．

(Ⅰ)求函数h(x)＝g(x)－f(x)的最大值；

(Ⅱ)对任意x1∈[1，e]，x2∈，是否存在实数k，使得不等式成立，若存在，请求出实数k的取值范围；若不存在，请说明理由．

Answer 1

【答案】(Ⅰ) ；(Ⅱ) .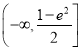

【解析】试题分析：（Ⅰ）由题意得方程组，解得a，b的值，设h（x）=g（x）﹣f（x）=lnx﹣x2+5，通过求导得出h（x）在（，+∞）递减，在（0， ）递增；从而求出函数h（x）的最大值．

（Ⅱ）设G（x）=2k[g（x）﹣2]+f（x）+3=2klnx+x2，通过讨论①k≥0，②0＜，③1＜≤e，④＞e的情况，从而求出k的范围．

试题解析：

(Ⅰ)点P(2,1)关于直线y＝x的对称点Q(1,2)，

∴，解得，

设h(x)＝g(x)－f(x)＝lnx－x2＋5，

h′(x)＝－2x

＝－＝－，

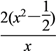∵x∈(0，＋∞)，

∴当x∈(，＋∞)时，h′(x)<0；当x∈(0，)时，h′(x)>0，

∴h(x)在(，＋∞)上单调递减；在(0，)上单调递增，

∴h(x)max＝h()＝－ln2，

(Ⅱ)设T(x)＝ln＝2lnx，

∵ T′(x)＝，当x∈[，e2]时，T′(x)>0，即单调递增，

∴在[，e2]上T(x)min＝T()＝lne＝1，

设G(x)＝2k＋f(x)＋3＝2klnx＋x2，

G′(x)＝＋2x＝，

①当k≥0时，在[1，e]上G′(x)>0，即单调递增，即G(x)max＝G(e)＝2k＋e2，

依题得2k＋e2≤1，∴k≤，

又∵k≥0，∴k无解；

②当0<≤1，即－1≤k<0时，

在[1，e]上G′(x)>0，即单调递增，

G(x)max＝G(e)＝2k＋e2 ，

依题得2k＋e2≤1，∴k≤，

又∵－1≤k<0，∴k无解；

③当1<≤e，即－e2≤k<－1时，

在[1，]上G′(x)<0，即单调递减；

在[，e]上 G′(x)>0，即单调递增，

又∵G(e)＝2k＋e2，G(1)＝1，

当G(e)≤G(1)，即k≤时，G(x)max＝G(1)＝1，显然1≤1成立；

∵－e2<<－1，∴－e2≤k≤；

当G(e)>G(1)，即k>时，G(x)max＝G(e)＝2k＋e2，

由2k＋e2≤1得k≤，∴k无解；

④当>e，即k<－e2时，在[1，e]上G′(x)<0，即单调递减，G(x)max＝G(1)＝1，显然1≤1成立，

综上，实数k的取值范围为.