题目内容
20.定义$\frac{n}{{a}_{1}+{a}_{2}+…+{a}_{n}}$为n个正数a1,a2,…,an的“均倒数”,若已知数列{an}的前n项的“均倒数”为$\frac{1}{2n+1}$,则an=4n-1.分析 通过“均倒数”的定义可知a1+a2+…+an=n•(2n+1)、a1+a2+…+an+an+1=(n+1)•(2n+3),两者作差计算即得结论.
解答 解:由题可知:$\frac{n}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{1}{2n+1}$,
∴a1+a2+…+an=n•(2n+1),
∴a1+a2+…+an+an+1=(n+1)•(2n+3),
两式相减得:an+1=(n+1)•(2n+3)-n•(2n+1)=4(n+1)-1,
又∵$\frac{1}{{a}_{1}}$=$\frac{1}{3}$,即a1=3满足上式,
∴an=4n-1,
故答案为:4n-1.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
10.若(1-2x)11=a0+a1x+a2x2+…+a11x11,则a2+a3+…+a11等于( )
| A. | 20 | B. | 16 | C. | -18 | D. | -17 |
5.若集合M={1},则满足M∪N={1,2}的集合N的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.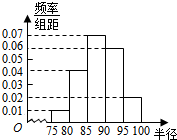 某盒里有20个球,其半径大小的频率分布直方图如图所示.
某盒里有20个球,其半径大小的频率分布直方图如图所示.
(Ⅰ)下表是这些球的半径的频数分布表,求正整数a,b的值;
(Ⅱ)半径在[90,95)和[95,100)里的球分别用1,2,3,…标记,现从这两个区间里的球中各摸出一球.
①若用x表示从区间[90,95)中摸出的球的号码,y表示从区间[95,100)中摸出的球的号码,请写出数对(x,y)的所有情形;
②求这两球的号码之和大于5的概率.
 某盒里有20个球,其半径大小的频率分布直方图如图所示.
某盒里有20个球,其半径大小的频率分布直方图如图所示.(Ⅰ)下表是这些球的半径的频数分布表,求正整数a,b的值;
| 区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
| 人数 | 1 | a | 7 | 6 | b |
①若用x表示从区间[90,95)中摸出的球的号码,y表示从区间[95,100)中摸出的球的号码,请写出数对(x,y)的所有情形;
②求这两球的号码之和大于5的概率.
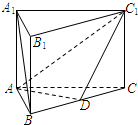 如图,在直三棱柱ABC-A1B1C1中,已知点D为棱BC中点.
如图,在直三棱柱ABC-A1B1C1中,已知点D为棱BC中点.