题目内容
8．
如图，在直三棱柱ABC-A1B1C1中，已知点D为棱BC中点．（1）如果AB=AC，求证：平面ADC1⊥平面BB1C1C；
（2）求证：A1B∥平面AC1D．
分析 （1）由CC1⊥平面ABC．可证CC1⊥AD，由AB=AC，D为BC中点，可证AD⊥BC，即可证明AD⊥平面BB1C1C从而可证平面AC1D⊥平面BB1C1C．
（2）连结A1C，设A1C∩AC1=E，连结DE．可得E为A1C中点，由D为BC中点，可证DE∥A1B，即可证明A1B∥平面AC1D．
解答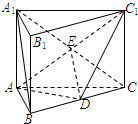 
证明：（1）在直三棱柱ABC-A1B1C1中，CC1⊥平面ABC．
因为AD?平面ABC，所以CC1⊥AD． …（2分）
因为AB=AC，D为BC中点，所以AD⊥BC．…（4分）
因为BC?平面BB1C1C，CC1?平面BB1C1C，BC∩CC1=C，
所以AD⊥平面BB1C1C．…（6分）
因为AD?平面AC1D，
所以平面AC1D⊥平面BB1C1C．…（8分）
（2）连结A1C，设A1C∩AC1=E，连结DE．
因为在直三棱柱ABC-A1B1C1中，四边形AA1C1C为平行四边形，
所以E为A1C中点． …（10分）
因为D为BC中点，所以DE∥A1B．…（12分）
因为DE?平面AC1D，A1B?平面AC1D，
所以A1B∥平面AC1D．…（14分）
点评 本题主要考查了直线与平面平行的判定，平面与平面垂直的判定，考查了空间想象能力和推理论证能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．已知一段演绎推理：“因为指数函数y=ax是增函数，而$y={（\frac{1}{2}）^x}$是指数函数，所以$y={（\frac{1}{2}）^x}$是增函数”，则这段推理的（ ）
| A． | 大前提错误 | B． | 小前提错误 | C． | 结论正确 | D． | 推理形式错误 |
19．设x∈（0，$\frac{π}{2}$），lgsin2x-lgsinx=lg$\frac{1}{2}$，则tanx等于（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{15}$ | D． | 5 |
16．若函数f（x）=x2+mx+m（m∈R）在（-2，+∞）上是增函数，则m的取值范围是（ ）
| A． | （-∞，4） | B． | （-∞，4] | C． | （4，+∞） | D． | [4，+∞） |
17．设$\overrightarrow a=（{x_1}，{y_1}）$，$\overrightarrow b=（{x_2}，{y_2}）$，则下列命题中错误的是（ ）
| A． | $|\overrightarrow a|=\sqrt{x_1^2+y_1^2}$ | B． | $\overrightarrow a•\overrightarrow b={x_1}{x_2}+{y_1}{y_2}$ | ||
| C． | $\overrightarrow a⊥\overrightarrow b?{x_1}{x_2}+{y_1}{y_2}=0$ | D． | $\overrightarrow a∥\overrightarrow b={x_1}{y_2}+{x_2}{y_1}=0$ |