题目内容
如图,在斜三棱柱 中,侧面
中,侧面 ,
,
 ,
, ,底面
,底面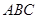 是边长为
是边长为 的正三角形,其重心为
的正三角形,其重心为 点,
点, 是线段
是线段 上一点,且
上一点,且 .
.
(1)求证: 侧面
侧面 ;
;
(2)求平面 与底面
与底面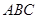 所成锐二面角的正切值.
所成锐二面角的正切值.
(1)证明:连接 并延长与
并延长与 交于
交于 点,则由题
点,则由题
意及相似关系可知点 为
为 的中点,所以
的中点,所以 三点共线,
三点共线,
从而可得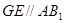 ,因此
,因此 侧面
侧面 ;
;
(2) .
.
解析试题分析:(1)要证明直线 侧面
侧面 ,即证明
,即证明 平行于侧面
平行于侧面 的某条直线,而由题意及相似关系易知
的某条直线,而由题意及相似关系易知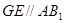 ,即可证明之;
,即可证明之;
(2)这问的关键是找出平面 与底面
与底面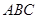 所成二面角的平面角,由侧面
所成二面角的平面角,由侧面 底面
底面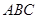 知,过
知,过 点作
点作 的垂线与
的垂线与 的延长线交于点
的延长线交于点 ,则
,则 平面
平面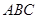 ,经过
,经过 点作
点作 的垂线与
的垂线与 的延长线交于点
的延长线交于点 ,则
,则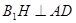 ,于是
,于是 即为所求二面角的平面角,然后根据相似关系可求该二面角的平面角的正切值.
即为所求二面角的平面角,然后根据相似关系可求该二面角的平面角的正切值.
试题解析:(1)证明:连接 并延长与
并延长与 交于
交于 点,则由题意及相似关系可知点
点,则由题意及相似关系可知点 为
为 的中点,
的中点,
所以 三点共线,从而可得
三点共线,从而可得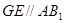 ,因此
,因此 侧面
侧面 .
.
(2)经过 点作
点作 的垂线与
的垂线与 的延长线交于点
的延长线交于点 ,则
,则 平面
平面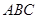 ,经过
,经过 点作
点作 的垂线与
的垂线与 的延长线交于点
的延长线交于点 ,则
,则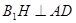 ,所以
,所以 即为所求二面角的平面角且
即为所求二面角的平面角且 ,则
,则 ,并由相似关系得:
,并由相似关系得: ,故
,故 ,即为所求二面角的正切值.
,即为所求二面角的正切值.
考点:与二面角有关的立体几何综合题;直线与平面平行的判定.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 中,
中, 丄平面
丄平面 ,
, 丄
丄 ,
, 丄
丄 ,
, ,
, ,
, .
. 丄
丄 的正弦值;
的正弦值; 外接球的体积.
外接球的体积.
 CD=1,PD=
CD=1,PD= .
.
 ?
?
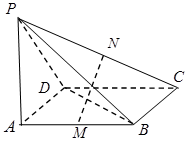

 =
= =2.求证:直线EG,FH,AC相交于一点.
=2.求证:直线EG,FH,AC相交于一点.
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ,
, 是正三角形,平面
是正三角形,平面 平面
平面 .
. ;
; 的体积.
的体积.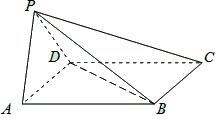
 ,则AB的中点M与C的距离为_ ▲ .
,则AB的中点M与C的距离为_ ▲ .