题目内容
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
(1)证明详见解析;(2)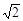 .
.
解析试题分析:(1) 由PD⊥平面ABCD,得PD⊥BC,由∠BCD=90°,得CD⊥BC,所以BC⊥平面PCD,那么PC⊥BC;(2)利用等积法,先求出棱锥的体积V=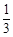 S△ABC·PD=
S△ABC·PD=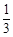 ,再求出S△PBC=
,再求出S△PBC=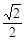 ,由
,由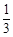 S△PBC·h=V=
S△PBC·h=V=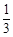 ,得h=
,得h=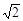 .
.
解:(1)证明:∵ PD⊥平面ABCD,BC 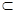 平面ABCD,∴ PD⊥BC. 1分
平面ABCD,∴ PD⊥BC. 1分
由∠BCD=90°,得CD⊥BC. 3分
又PD∩DC=D, PD,DC 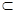 平面PCD,
平面PCD,
∴ BC⊥平面PCD. 5分
∵ PC 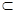 平面PCD,故PC⊥BC. 7分
平面PCD,故PC⊥BC. 7分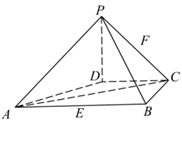
(2)连接AC,设点A到平面PBC的距离为h.
∵ AB∥DC,∠BCD=90°,∴∠ABC=90°. 8分
由AB=2,BC=1,得△ABC的面积S△ABC=1. 9分
由PD⊥平面ABCD,及PD=1,得三棱锥P-ABC的体积
V=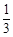 S△ABC·PD=
S△ABC·PD=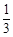 . 10分
. 10分
∵ PD⊥平面ABCD,DC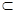 平面ABCD,∴ PD⊥DC. ....11分
平面ABCD,∴ PD⊥DC. ....11分
又∴PD=DC=1,∴PC=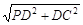 =
=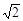 .由PC⊥BC,BC=1,
.由PC⊥BC,BC=1,
得△PBC的面积S△PBC=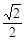 . .. ..12分
. .. ..12分
∵VA - PBC=VP - ABC,
∴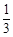 S△PBC·h=V=
S△PBC·h=V=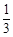 ,得h=
,得h=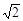 . .13分
. .13分
故点A到平面PBC的距离等于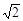 . 14分
. 14分
考点:1.线、面之间的平行与垂直关系的判定与性质;2.三棱锥的体积.

 阅读快车系列答案
阅读快车系列答案 平面
平面 ,四边形
,四边形 为矩形,
为矩形, .
. 为
为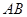 的中点,
的中点, .(1)求证:
.(1)求证: ;(2)若
;(2)若 与平面
与平面 所成的角为
所成的角为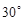 ,求二面角
,求二面角 的余弦值.
的余弦值.
 中,侧面
中,侧面 ,
,
 ,
, ,底面
,底面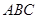 是边长为
是边长为 的正三角形,其重心为
的正三角形,其重心为 点,
点, 是线段
是线段 上一点,且
上一点,且 .
.
 侧面
侧面 ;
; 与底面
与底面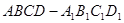 中,已知平面
中,已知平面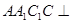 平面
平面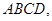 且
且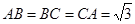 ,
,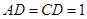 .
.
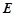 为棱
为棱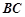 上的一点,且
上的一点,且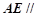 平面
平面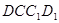 ,求线段
,求线段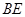 的长度
的长度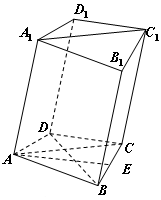
 为正方形,
为正方形, 平面
平面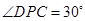 ,
, 于点
于点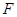 ,
, ,交
,交 于点
于点 .
.
 平面
平面 ;
;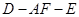 的余弦值.
的余弦值. 中,
中, ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,
, 分别为线段
分别为线段 的中点.
的中点.
 ;
;  ⊥平面
⊥平面 .
. 的大小为
的大小为 ,菱形
,菱形 在面
在面 内,
内,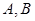 两点在棱
两点在棱 上,
上, ,
, 是
是 的中点,
的中点, 面
面 ,垂足为
,垂足为 .
. 平面
平面 ;
; 与
与 所成角的余弦值.
所成角的余弦值.
 ,
, 为直角,
为直角, ,
, ,现以其中一直角边
,现以其中一直角边 为轴,按逆时针方向旋转
为轴,按逆时针方向旋转 后,将
后,将 点所在的位置记为
点所在的位置记为 ,再按逆时针方向继续旋转
,再按逆时针方向继续旋转 后,
后, .
. ,取
,取 ,求证:面
,求证:面 面
面 ;
; 与平面
与平面
 的底面是边长为1的正方形,且侧棱垂直于底面,若
的底面是边长为1的正方形,且侧棱垂直于底面,若 与底面
与底面 成60°角,则二面角
成60°角,则二面角 的平面角的正切值为
的平面角的正切值为