题目内容
如图,在四棱锥 中,
中, 丄平面
丄平面 ,
, 丄
丄 ,
, 丄
丄 ,
, ,
, ,
, .
.
(Ⅰ)证明: 丄
丄 ;
;
(Ⅱ)求二面角 的正弦值;
的正弦值;
(Ⅲ)求三棱锥 外接球的体积.
外接球的体积.
(1)证明见解析;(2)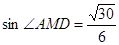 ;(3)
;(3)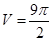 .
.
解析试题分析:(1)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等;(2)作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角;(3)利用棱锥的体积公式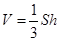 求体积,注意转化为特殊几何体,如长方体、正方体等.
求体积,注意转化为特殊几何体,如长方体、正方体等.
试题解析:解:(Ⅰ)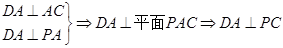 .................4分
.................4分
(Ⅱ)过 作
作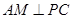 交
交 于点
于点 ,连接
,连接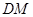 ,则
,则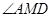 为所求角
为所求角
在三角形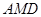 中,
中,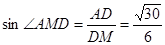 ........................8分
........................8分
(Ⅲ)求三棱锥 外接球即为以
外接球即为以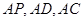 为棱的长方体的外接球,长方体的对角线为球的直径
为棱的长方体的外接球,长方体的对角线为球的直径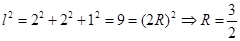
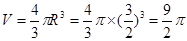 ...............12分
...............12分
考点:(1)直线与直线垂直;(2)二面角的求法;(3)求外接球的体积.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 平面ABCD,BF=3,G、H分别是CE和CF的中点.
平面ABCD,BF=3,G、H分别是CE和CF的中点.

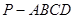 中,底面
中,底面 是正方形,
是正方形,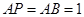 ,
,  ,
, 分别是
分别是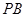 ,
,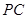 的中点.
的中点.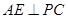
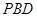 的距离.
的距离.

 平面
平面 ,四边形
,四边形 为矩形,
为矩形, .
. 为
为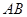 的中点,
的中点, .(1)求证:
.(1)求证: ;(2)若
;(2)若 与平面
与平面 所成的角为
所成的角为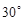 ,求二面角
,求二面角 的余弦值.
的余弦值.
 中,侧面
中,侧面 ,
,
 ,
, ,底面
,底面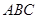 是边长为
是边长为 的正三角形,其重心为
的正三角形,其重心为 点,
点, 是线段
是线段 上一点,且
上一点,且 .
.
 侧面
侧面 ;
; 与底面
与底面 的大小为
的大小为 ,菱形
,菱形 在面
在面 内,
内,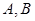 两点在棱
两点在棱 上,
上, ,
, 是
是 的中点,
的中点, 面
面 ,垂足为
,垂足为 .
. 平面
平面 ;
; 与
与 所成角的余弦值.
所成角的余弦值.
 的底面是边长为1的正方形,且侧棱垂直于底面,若
的底面是边长为1的正方形,且侧棱垂直于底面,若 与底面
与底面 成60°角,则二面角
成60°角,则二面角 的平面角的正切值为
的平面角的正切值为