题目内容
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF  平面ABCD,BF=3,G、H分别是CE和CF的中点.
平面ABCD,BF=3,G、H分别是CE和CF的中点.
(Ⅰ)求证:AF//平面BDGH;
(Ⅱ)求 

(Ⅰ)见解析(Ⅱ)1
解析试题分析:(Ⅰ)连结AC、BD,设AC、BD交于O,连结HO,由ABCD为正方形知,O是AC的中点,由H是CF的中点及三角形中位线定理知,OH∥AF,由线面平行判定定理知,AF∥面BDGH;
(Ⅱ)由BDEF为矩形知DE⊥BD,由面BDEF⊥面ABCD及面面垂直性质定理知DE⊥面ABCD,所以DE⊥AC,由ABCD为正方形知AC⊥BD,所以AC⊥面BDEF,AO是A到面BDEF的距离,因为H是CF的中点,所以H到面BDEF的距离为AO的一半,很容易计算出棱锥H-BEF的体积就是棱锥E-BFH的体积.
试题解析:(Ⅰ) 证明:设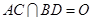 ,连接
,连接 ,
,
在 中,因为
中,因为 ,
, ,
,
所以 ,
,
又因为 平面
平面 ,
, 平面
平面 ,
,
所以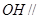 平面
平面 . (6分)
. (6分)
(Ⅱ)因为四边形 是正方形,
是正方形,
所以 .
.
又因为平面 平面
平面 ,平面
,平面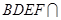 平面
平面 ,
,
且 平面
平面 ,
,
所以 平面
平面 . 得
. 得  平面
平面 (8分)
(8分)
则H到平面 的距离为CO的一半
的距离为CO的一半
又因为 ,三角形
,三角形 的面积
的面积 ,
,
所以 (12分)
(12分)
考点:线面平行的判定,面面垂直性质定理,线面垂直的判定与性质,锥体体积计算,推理论证能力

练习册系列答案
相关题目
 中,
中, 于
于 ,三边分别是
,三边分别是 ,则有
,则有 ;类比上述结论,写出下列条件下的结论:四面体
;类比上述结论,写出下列条件下的结论:四面体 中,
中, 的面积分别是
的面积分别是 ,二面角
,二面角 的度数分别是
的度数分别是 ,则
,则 .
. 中,底面
中,底面 且边长为
且边长为 的菱形,侧面
的菱形,侧面 是等边三角形,且平面
是等边三角形,且平面
 为
为 的中点,求证:
的中点,求证: 平面
平面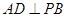 ;
; 的大小.
的大小. 中,
中, 丄平面
丄平面 丄
丄 丄
丄 ,
, ,
, ,
, .
. 丄
丄 的正弦值;
的正弦值; 外接球的体积.
外接球的体积.
 CD=1,PD=
CD=1,PD= .
.
 ?
? =
= =2.求证:直线EG,FH,AC相交于一点.
=2.求证:直线EG,FH,AC相交于一点.
 在二面角
在二面角 的棱上,点
的棱上,点 在
在 内,且
内,且 .若对于
.若对于 内异于
内异于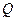 ,都有
,都有 ,则二面角
,则二面角 ,则AB的中点M与C的距离为_ ▲ .
,则AB的中点M与C的距离为_ ▲ . 与矩形
与矩形 所在的平面互相垂直,将
所在的平面互相垂直,将 沿
沿 翻折,翻折后的点E恰与BC上的点P重合.设
翻折,翻折后的点E恰与BC上的点P重合.设 ,则当
,则当 时,
时, 有最小值.
有最小值.