题目内容
已知：
中，
于
，三边分别是
，则有
；类比上述结论，写出下列条件下的结论：四面体
中，，
的面积分别是
，二面角
的度数分别是
，则
．
s1cos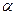
+s2co
s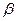
+s3cos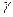
解析
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
已知：中，于，三边分别是，则有；类比上述结论，写出下列条件下的结论：四面体中，，的面积分别是，二面角的度数分别是，则 ．
s1cos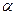+s2cos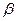+s3cos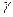
解析
名校课堂系列答案
平面ABCD，BF=3，G、H分别是CE和CF的中点．
中，底面
是正方形，
⊥平面
， 
，
分别是
,
的中点.
到平面
的距离.
平面
，四边形
为矩形，
．
为
的中点，
.（1）求证：
；（2）若
与平面
所成的角为
，求二面角
的余弦值.
中,
⊥平面
,
∥
，
,
分别为线段
的中点.
; 
⊥平面
.
ABC中，两直角边分别为a,b,斜边上的高为h,则得
”由此可类比出命题“若三棱锥S-ABC的三条侧棱SA，SB，SC两两垂直，长分别为a,b,c，底面ABC上的高为h,则得____________________.
的底面是边长为1的正方形，且侧棱垂直于底面，若
与底面
成60°角，则二面角
的平面角的正切值为
中，
，
、
分别是
、
的中点，
，则异面直线
、
所成的角为 ．