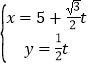Question

【题目】如图，在直三棱柱ABC﹣A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．
（Ⅰ）求证：平面ABC1⊥平面A1C1CA；
（Ⅱ）设D是A1C1的中点，判断并证明在线段BB1上是否存在点E，使DE∥平面ABC1；若存在，求三棱锥E﹣ABC1的体积．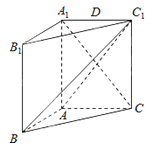

Answer 1

【答案】证明：（I）在直三棱柱ABC﹣A1B1C1中，有AA1⊥平面ABC．
∴AA1⊥AC，又AA1=AC，∴A1C⊥AC1 ．
又BC1⊥A1C，∴A1C⊥平面ABC1 ，
∵A1C平面A1C1CA，
∴平面ABC1⊥平面A1C1CA．
（II）解：取AA1中点F，连EF，FD，当E为B1B中点时，EF∥AB，DF∥AC1 ．
即平面EFD∥平面ABC1 ， 则有ED∥平面ABC1 ．
当E为中点时，V E﹣ABC1=VC1﹣ABE=x2xx1x1=．

【解析】（Ⅰ）证明平面ABC1⊥平面A1C，只需证明A1C⊥平面ABC1；
（Ⅱ）取AA1中点F，连EF，FD，证明平面EFD∥平面ABC1 ， 则有ED∥平面ABC1 ， 利用等体积转换，可求三棱锥E﹣ABC1的体积．
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识，掌握一个平面过另一个平面的垂线，则这两个平面垂直．