题目内容
8.在△ABC中,角A、B、C的对边分别是a、b、c,点(a,b)在直线x(sinA-sinB)+ysinB=csinC上.(1)求C的大小;
(2)若c=7,求△ABC的周长的取值范围.
分析 (1)把点(a,b)代入直线方程,利用正弦定理进行化简后求出cosC的值,由内角的范围即可求出C;
(2)利用余弦定理和基本不等式化简,求出a+b的范围,再由三边的关系求出△ABC周长的取值范围.
解答 解:(1)由题意得,点(a,b)在直线x(sinA-sinB)+ysinB=csinC上,
∴a(sinA-sinB)+bsinB=csinC,
根据正弦定理得,a(a-b)+b2=c2,
整理得,ab=a2+b2-c2,则cosC=$\frac{1}{2}$,
由0<C<π得,C=$\frac{π}{3}$;
(2)由(1)和余弦定理得,c2=a2+b2-2abcosC=a2+b2-ab
则49=(a+b)2-3ab≥${(a+b)}^{2}-\frac{3}{4}(a+b)^{2}=\frac{1}{4}(a+b)^{2}$,
∴(a+b)2≤4×49,则a+b≤14(当且仅当a=b时等号成立),
∵a+b>7,c=7,
∴△ABC的周长的取值范围是(14,21].
点评 本题考查了正弦、余弦定理,三角形三边关系,以及基本不等式的综合应用,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
3.下列函数中,在其定义域内,既是奇函数又是减函数的是( )
| A. | f(x)=-x3 | B. | f(x)=$\sqrt{-x}$ | C. | f(x)=-tanx | D. | f(x)=$\frac{1}{x}$ |
20.某几何体的三视图如图所示,且该几何体的体积是2,则正视图中的x=( )
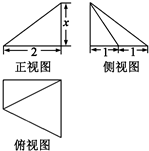

| A. | 2 | B. | 3 | C. | $\frac{4}{15}$ | D. | $\frac{4}{5}$ |
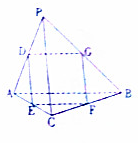 如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.
如图,已知三棱锥P-ABC中,点D,E,F,G分别是棱AP,AC,BC,PB上的点,若PA=PB=PC=$\sqrt{2}$,AB=AC=BC=1,且$\frac{AE}{AC}$=$\frac{AD}{AP}$=$\frac{BF}{BC}$=$\frac{BG}{BP}$.