题目内容
抛物线y=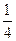 x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.
x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.
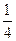 x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.
x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.(±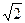 ,
,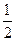 )
)
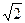 ,
,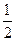 )
)方程即x2=4y,由抛物线定义可知,点P到顶点O和焦点F的距离相等,∴点P为线段OF中垂线与抛物线的交点,令y=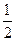 得x=±
得x=±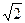 ,∴P(±
,∴P(±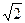 ,
,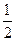 ).
).
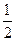 得x=±
得x=±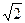 ,∴P(±
,∴P(±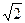 ,
,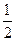 ).
).
练习册系列答案
相关题目
题目内容
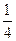 x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.
x2上一点P到其顶点和准线距离相等,则点P的坐标是_________________.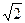 ,
,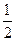 )
)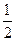 得x=±
得x=±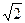 ,∴P(±
,∴P(±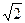 ,
,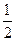 ).
).