题目内容
设函数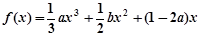 ,
, ,
,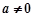 .
.
(1)若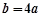 ,求
,求 的单调递增区间;
的单调递增区间;
(2)若曲线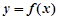 与
与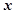 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且 的极小值为
的极小值为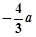 ,求
,求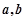 的值.
的值.
(1)证明过程详见解析(2) 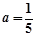 ,
,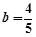 .
.
解析试题分析:
(1)将条件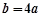 带入函数解析式消b,得到
带入函数解析式消b,得到 ,对该三次函数求导得到导函数,由于
,对该三次函数求导得到导函数,由于 ,故该导函数为二次函数,根据题意需要求的该二次函数大于0的解集,因为二次函数含参数,故依次讨论开口,
,故该导函数为二次函数,根据题意需要求的该二次函数大于0的解集,因为二次函数含参数,故依次讨论开口, 的符号和根的大小,即可到导函数大于0的解集即为原函数的单调增区间.
的符号和根的大小,即可到导函数大于0的解集即为原函数的单调增区间.
(2)分析题意,可得该三次函数过原点,根据函数 与x轴相切,所以有个极值为0且有一个重根,故可得函数
与x轴相切,所以有个极值为0且有一个重根,故可得函数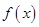 有一个极大值0和一个极小值
有一个极大值0和一个极小值 ,有一个重根,则对
,有一个重根,则对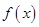 因式分解会得到完全平方式,即
因式分解会得到完全平方式,即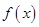 提取x的公因式后,剩下二次式的判别
提取x的公因式后,剩下二次式的判别 ,得到a,b之间的关系式,再根据极小值为
,得到a,b之间的关系式,再根据极小值为 ,则求导求出极小值点,得到关于a,b的另外一个等式,即可求出a,b的值.
,则求导求出极小值点,得到关于a,b的另外一个等式,即可求出a,b的值.
试题解析:
(1) ,
,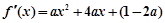 .
.
令 ,
,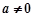 ,
,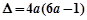
当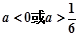 时,由
时,由 得
得 .
.
①当 时,
时, 的单调递增区间为
的单调递增区间为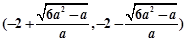 ; 3分
; 3分
②当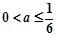 时,
时, 的单调递增区间为
的单调递增区间为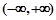 ; 5分
; 5分
③当 时,
时, 的单调递增区间为
的单调递增区间为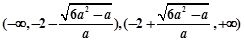 . 7分
. 7分
(2) ,
,
依据题意得: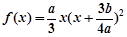 ,且
,且 ① 9分
① 9分 ,得
,得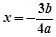 或
或 . 11分
. 11分
因为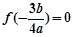 ,所以极小值为
,所以极小值为 ,
,
∴ 且
且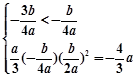 ,得
,得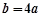 , 13分
, 13分
代入①式得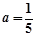 ,
,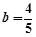 . 15分
. 15分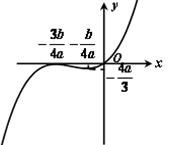
考点: 含参二次不等式 导数 极值

练习册系列答案
相关题目
 上给定曲线
上给定曲线 ,试在此区间内确定点
,试在此区间内确定点 的值,使图中所给阴影部分的面积
的值,使图中所给阴影部分的面积 与
与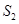 之和最小.
之和最小.
 .
.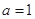 ,求函数
,求函数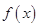 的单调区间;
的单调区间;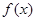 在区间
在区间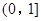 上是减函数,求实数
上是减函数,求实数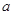 的取值范围;
的取值范围;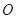 作曲线
作曲线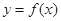 的切线,证明:切点的横坐标为
的切线,证明:切点的横坐标为 .
. 处取得极值2
处取得极值2 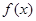 的表达式;
的表达式; 满足什么条件时,函数
满足什么条件时,函数 上单调递增?
上单调递增?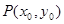 为
为 图象上任意一点,直线与
图象上任意一点,直线与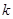 的取值范围
的取值范围  .
.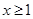 时,求
时,求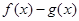 的最大值;
的最大值;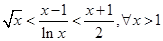 恒成立;
恒成立;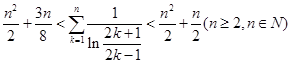 .(参考数据:
.(参考数据: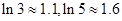 )
)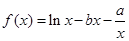 (
( 、
、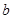 为常数),在
为常数),在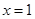 时取得极值.
时取得极值.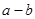 的值;
的值;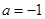 时,求函数
时,求函数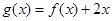 的最小值;
的最小值;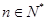 时,试比较
时,试比较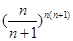 与
与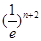 的大小并证明.
的大小并证明.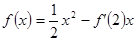 ,
,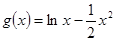 。
。 的解析式;
的解析式; ,都有
,都有 成立,求实数
成立,求实数 的取值范围;
的取值范围;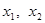 ,
, ,且
,且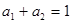 ,求证:
,求证: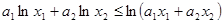 。
。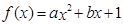 在
在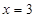 处的切线方程为
处的切线方程为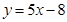 .
. 的解析式;
的解析式; 的方程
的方程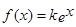 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数 的值;
的值; 满足
满足 ,
,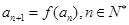 ,求
,求 的整数部分.
的整数部分.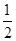 m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1. 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;