题目内容
在区间 上给定曲线
上给定曲线 ,试在此区间内确定点
,试在此区间内确定点 的值,使图中所给阴影部分的面积
的值,使图中所给阴影部分的面积 与
与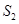 之和最小.
之和最小.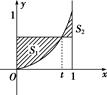
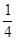 .
.
解析试题分析:先由定积分的几何意义分别求出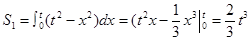 ,
,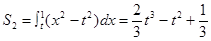 ,从而
,从而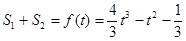
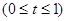 ,然后通过导数确定函数
,然后通过导数确定函数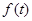 的极值,并求出端点值,比较极值与端点值的大小,最小的就是最小值,问题就解决了.
的极值,并求出端点值,比较极值与端点值的大小,最小的就是最小值,问题就解决了.
试题解析:设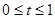
当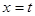 时,
时,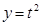
∴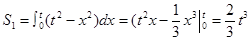
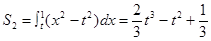
∴阴影部分的面积为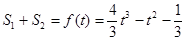
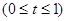
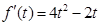 ,令
,令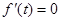 可得
可得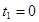 或
或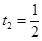
由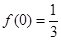 ,
, 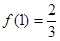
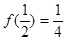
可知当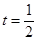 时,
时,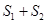 有最小值
有最小值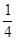 .
.
考点:1.定积分的几何意义;2.函数的最值与导数.

练习册系列答案
相关题目
 在(0,1)上单调递减.
在(0,1)上单调递减. ,求
,求 在[1,2]上的最小值.
在[1,2]上的最小值. (如图所示,其中O为圆心,
(如图所示,其中O为圆心,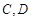 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).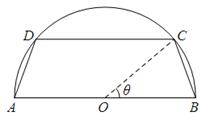
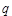 的值,使体积V最大;
的值,使体积V最大;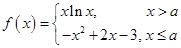 ,其中
,其中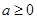 .
.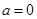 时,求函数
时,求函数 的图象在点
的图象在点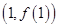 处的切线方程;
处的切线方程; 、
、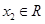 ,且
,且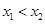 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.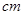 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料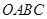 ,其中点
,其中点 在圆弧上,点
在圆弧上,点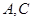 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以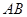 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设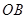 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为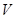
 .
.
 型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算,
型卡车将某种水果运送(满载)到相距400km的水果批发市场.据测算, (单位:
(单位: )与速度
)与速度 (单位:km/h)的关系近似地满足
(单位:km/h)的关系近似地满足 ,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L.
,除燃油费外,人工工资、车损等其他费用平均每小时300元.已知燃油价格为7.5元/L. (元)(不计返程费用),将
(元)(不计返程费用),将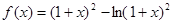 ,
,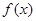 的单调区间;
的单调区间;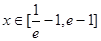 时,不等式
时,不等式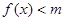 恒成立,求实数
恒成立,求实数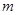 的取值范围;
的取值范围; 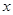 的方程
的方程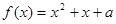 在区间
在区间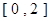 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数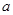 的取值范围.
的取值范围.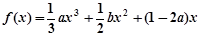 ,
, ,
,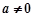 .
. 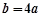 ,求
,求 的单调递增区间;
的单调递增区间;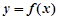 与
与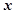 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且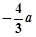 ,求
,求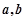 的值.
的值.