题目内容
已知 .
.
(1)当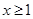 时,求
时,求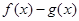 的最大值;
的最大值;
(2)求证: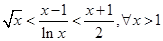 恒成立;
恒成立;
(3)求证: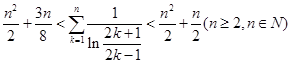 .(参考数据:
.(参考数据: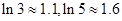 )
)
(1)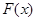 的最大值为0;(2)详见解析;(3)详见解析.
的最大值为0;(2)详见解析;(3)详见解析.
解析试题分析:(1)设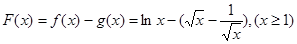 ,求导利用单调性即可得其最大值;.
,求导利用单调性即可得其最大值;.
(2)由(1)得,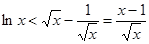 ,变形即得左边的不等式:
,变形即得左边的不等式: .右边不等式显然不宜直接作差,故考虑作适当的变形.为了证右边,设
.右边不等式显然不宜直接作差,故考虑作适当的变形.为了证右边,设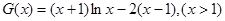 .求导得
.求导得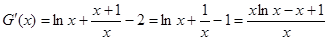 .
.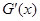 的符号还不能直接确定.为了确定
的符号还不能直接确定.为了确定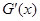 的符号,再设
的符号,再设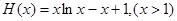 ,求导得
,求导得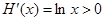 ,所以
,所以 即
即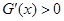 由此可知
由此可知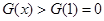 即
即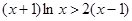 ,从而原命题得证;(3)首先看看所证不等式与第(2)题有何联系.对照待证不等式,可将(2)题中的不等式变形为:
,从而原命题得证;(3)首先看看所证不等式与第(2)题有何联系.对照待证不等式,可将(2)题中的不等式变形为: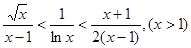 .显然取
.显然取 ,得
,得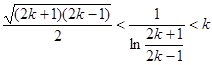 .右边易证如下:
.右边易证如下: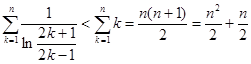 ;左边则应考虑做缩小变形.由于左边为
;左边则应考虑做缩小变形.由于左边为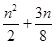 ,故将
,故将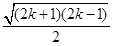 缩为一个等差数列.因为
缩为一个等差数列.因为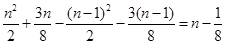 ,所以考虑把
,所以考虑把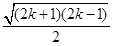 缩小为
缩小为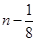 .
.
当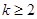 时,
时,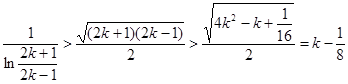 ,这样累加,再用等差数列的求和公式即可使问题得证.
,这样累加,再用等差数列的求和公式即可使问题得证.
试题解析:(1)设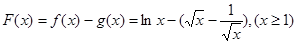 ,则
,则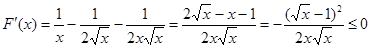 ,
,
所以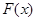 在区间
在区间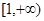 内单调递减,故
内单调递减,故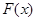 的最大值为
的最大值为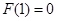 ; (4分)
; (4分)
(2)由(1)得,对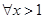 ,都有
,都有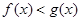 ,即
,即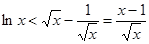 ,
,
因为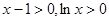 ,所以
,所以 . (6分)
. (6分)
设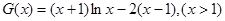 ,则
,则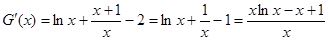 .
.
设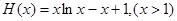 ,则
,则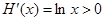 ,
,
所以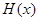 在区间
在区间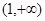 内单调递增,故
内单调递增,故 即
即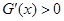 .
.
所以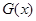 在区间
在区间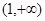 内单调递增,故
内单调递增,故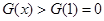 即
即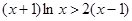 ,
,
因为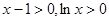 ,所以
,所以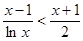 .
.
从而原命题得证. (9分)
(3)由(2)得,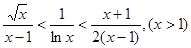 ,
,
令 ,得
,得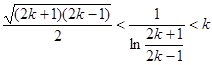 .
.
所以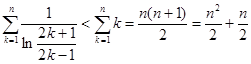 ; (11分)
; (11分)
另一方面,当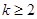 时,
时,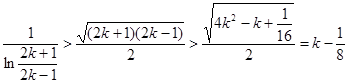 ,
,
所以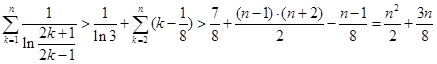
从而命题得证. (14分)
考点:1、导数及其应用;2、不等式的证明.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
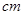 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料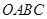 ,其中点
,其中点 在圆弧上,点
在圆弧上,点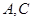 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以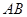 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设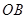 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为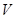
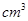 .
.
 (如图所示,其中O为圆心,
(如图所示,其中O为圆心,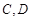 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).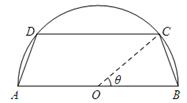
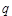 的值,使体积V最大;
的值,使体积V最大;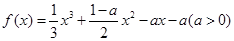 .
.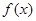 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;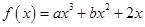 在
在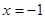 处取得极值,且在点
处取得极值,且在点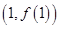 处的切线斜率为
处的切线斜率为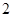 .
.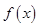 的单调增区间;
的单调增区间; 的方程
的方程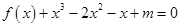 在区间
在区间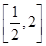 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数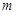 的取值范围.
的取值范围.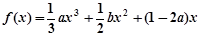 ,
, ,
,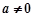 .
. 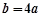 ,求
,求 的单调递增区间;
的单调递增区间;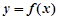 与
与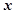 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且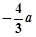 ,求
,求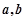 的值.
的值.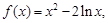
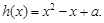
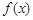 的极值;
的极值;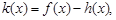 若函数
若函数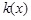 在
在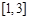 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数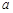 的取值范围.
的取值范围.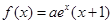 (其中
(其中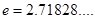 ),
),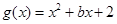 ,已知它们在
,已知它们在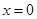 处有相同的切线.
处有相同的切线.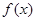 ,
,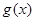 的解析式;
的解析式;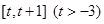 上的最小值;
上的最小值;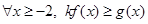 恒成立,求实数
恒成立,求实数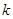 的取值范围.
的取值范围.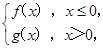 若方程G(x)=a2有且仅有四个解,求实数a的取值范围.
若方程G(x)=a2有且仅有四个解,求实数a的取值范围.