题目内容
9.执行如图所示的程序框图,若输出S的值为$\frac{2014}{2015}$,则判断框内可填入的条件是( )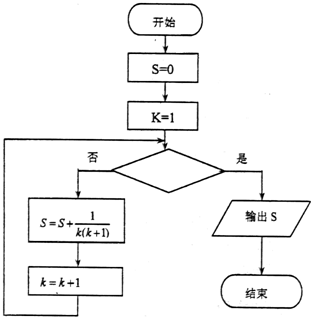
| A. | k>2013 | B. | k>2014 | C. | k>2015 | D. | k>2016 |
分析 根据程序的功能进行求解即可.
解答 解:本程序的功能是计算S=$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{k(k+1)}$=1$-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{k}$-$\frac{1}{k+1}$=1-$\frac{1}{k+1}$,
由1-$\frac{1}{k+1}$=$\frac{2014}{2015}$,得$\frac{1}{k+1}$=$\frac{1}{2015}$,
即k+1=2015,即k=2014,
即k=2014不成立,k=2015成立,
故断框内可填入的条件k>2014,
故选:B
点评 本题主要考查程序框图的识别和判断,根据裂项法进行求和是解决本题的关键.

练习册系列答案
相关题目
19.通过随机询问某校110名高中生在购买食物时是否看营养说明,得如下列联表:
(1)从这50名女生中按是否看营养说明分层抽样,抽取一个容量为5的样本,问样本中看与不看营养说明的女生各有多少名?
(2)根据以上列联表,问能否在犯错误的概率不超过0.010的前提下认为“性别与在购物时看营养说明有关系”${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,参考数据:
| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)根据以上列联表,问能否在犯错误的概率不超过0.010的前提下认为“性别与在购物时看营养说明有关系”${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,参考数据:
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
17.使函数y=xsinx+cosx是增函数的区间可能是( )
| A. | ($\frac{π}{2}$,$\frac{3π}{2}$) | B. | (π,2π) | C. | ($\frac{3π}{2}$,$\frac{5π}{2}$) | D. | (2π,3π) |
14.利用独立性检验来考虑两个分类变量X与Y是否有关系时,通过查阅下表来确定“X和Y有关系”的可信度.如果k>3.841,那么就有把握认为“X和Y有关系”的百分比为( )
| p(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 25% | B. | 97.5% | C. | 5% | D. | 95% |