题目内容
14.利用独立性检验来考虑两个分类变量X与Y是否有关系时,通过查阅下表来确定“X和Y有关系”的可信度.如果k>3.841,那么就有把握认为“X和Y有关系”的百分比为( )| p(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | 25% | B. | 97.5% | C. | 5% | D. | 95% |
分析 根据所给的观测值,把观测值同表格所给的临界值进行比较,看观测值大于哪一个临界值,得到说明两个变量有关系的可信程度.
解答 解:∵k>3.841,
∴有0.05的几率说明这两个变量之间的关系是不可信的,
即有1-0.05=95%的把握说明两个变量之间有关系,
故选D.
点评 本题考查独立性检验,考查两个变量之间的关系的可信程度,考查临界值表的应用,本题是一个基础题,关键在于理解临界值表的意义,而没有要我们求观测值,降低了题目的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(16名女员工,14名男员工)的得分,如下表:
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
(3)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?(参考数据请看15题中的表)
| 女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
| 男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
| “满意”的人数 | “不满意”人数 | 合计 | |
| 女 | 16 | ||
| 男 | 14 | ||
| 合计 | 30 |
9.执行如图所示的程序框图,若输出S的值为$\frac{2014}{2015}$,则判断框内可填入的条件是( )
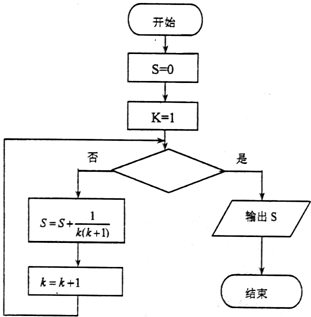

| A. | k>2013 | B. | k>2014 | C. | k>2015 | D. | k>2016 |
19.已知集合A={0,1,2,3},则满足A∪B=A的非空集合B的个数是( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
6.用反证法证明命题“三角形三个内角至少有一个不大于60°”时,应假设( )
| A. | 三个内角都不大于60° | B. | 三个内角都大于60° | ||
| C. | 三个内角至多有一个大于60° | D. | 三个内角至多有两个大于60° |
3.函数y=2x3-3x2( )
| A. | 在x=0处取得极大值0,但无极小值 | |
| B. | 在x=1处取得极小值-1,但无极大值 | |
| C. | 在x=0处取得极大值0,在x=1处取得极小值-1 | |
| D. | 以上都不对 |