题目内容
19.通过随机询问某校110名高中生在购买食物时是否看营养说明,得如下列联表:| 男 | 女 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)根据以上列联表,问能否在犯错误的概率不超过0.010的前提下认为“性别与在购物时看营养说明有关系”${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,参考数据:
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
分析 (1)先求出每个个体被抽到的概率,再用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数.
(2)根据性别与看营养说明列联表,求出K2的观测值k的值为7.486>6.635,再根据P(K2≥6.635)=0.01,该校高中学生“性别与在购买食物时看营养说明”有关.
解答 解:(1)根据分层抽样可得:样本中看营养说明的女生有$\frac{10}{50}$×30=6名,样本中不看营养说明的女生有$\frac{10}{50}×20$=4名;
(2)假设H0:该校高中学生性别与在购买食物时看营养说明无关,则K2应该很小.
根据题中的列联表得K2=$\frac{110×(50×20-30×10)^{2}}{80×30×60×50}$≈7.486
由P(K2≥6.635)=0.010可知在犯错误的概率不超过0.010的前提下认为性别与是否看营养说明之间有关系.
点评 本题主要考查抽样方法、随机事件的概率,独立性检验等知识,考查运用概率统计知识解决简单实际问题的能力,考查学生的数据处理的能力及应用意识.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
9.若函数f(x)=2sin(ωx+$\frac{π}{4}$)(ω>0)与g(x)=2cos(2x-$\frac{π}{4}$)的对称轴完全相同,则函数f(x)=2sin(ωx+$\frac{π}{4}$)(ω>0)在[0,π]上的递增区间是 ( )
| A. | [0,$\frac{π}{8}$] | B. | [0,$\frac{π}{4}$] | C. | [$\frac{π}{8}$,π] | D. | [$\frac{π}{4}$,π] |
10.已知f(x)=x3-ax在(-∞,-1]上递增,则a的取值范围是( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
7.已知某海滨浴场海浪的高度y(米)是时间t (0≤t≤24,单位:小时)函数,记作:y=f(t),下表是某日各时的浪高数据:
经长期观察,y=f(t)的曲线,可以近似地看成函数y=Acos(ωt)+b的图象.
(1)根据以上数据(对浪高采用精确到0.1的数据),求出函数y=Acos(ωt)+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
(参考数据cos$\frac{7π}{16}$≈0.2).
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.41 | 0.88 | 0.39 | 0.91 | 1.38 | 0.90 | 0.42 | 0.89 | 1.40 |
(1)根据以上数据(对浪高采用精确到0.1的数据),求出函数y=Acos(ωt)+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
(参考数据cos$\frac{7π}{16}$≈0.2).
8.sin$\frac{20π}{3}$=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
9.执行如图所示的程序框图,若输出S的值为$\frac{2014}{2015}$,则判断框内可填入的条件是( )
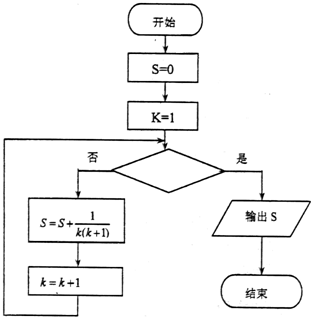

| A. | k>2013 | B. | k>2014 | C. | k>2015 | D. | k>2016 |