题目内容
16. 如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.
如图,在直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=AD=$\frac{1}{2}$CD=2,$\overrightarrow{CB}$=3$\overrightarrow{CM}$,则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12.
分析 首先分别以DC,DA二直线为x,y轴,建立平面直角坐标系,求出A,B,C,D四点的坐标,设M(x,y),根据$\overrightarrow{CB}=3\overrightarrow{CM}$即可求出M点坐标,从而可求得$\overrightarrow{DM}$,$\overrightarrow{AC}$的坐标,然后进行数量积的坐标运算即可.
解答 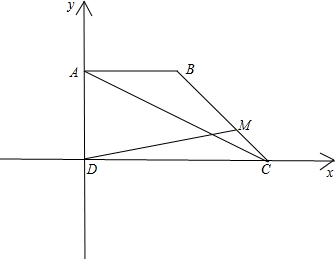 解:如图,分别以边DC,DA所在直线为x,y轴,建立平面直角坐标系,则:
解:如图,分别以边DC,DA所在直线为x,y轴,建立平面直角坐标系,则:
A(0,2),B(2,2),C(4,0),D(0,0);
设M(x,y),则$\overrightarrow{CM}=(x-4,y)$,$\overrightarrow{CB}=(-2,2)$;
∵$\overrightarrow{CB}=3\overrightarrow{CM}$;
∴(-2,2)=3(x-4,y);
∴$\left\{\begin{array}{l}{-2=3x-12}\\{2=3y}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x=\frac{10}{3}}\\{y=\frac{2}{3}}\end{array}\right.$;
∴$M(\frac{10}{3},\frac{2}{3})$;
∴$\overrightarrow{DM}=(\frac{10}{3},\frac{2}{3})$,$\overrightarrow{AC}=(4,-2)$;
∴$\overrightarrow{DM}•\overrightarrow{AC}=\frac{40}{3}-\frac{4}{3}=12$.
故答案为:12.
点评 考查通过建立平面直角坐标系求向量数量积的方法,根据点的坐标求向量的坐标,向量坐标的数乘运算,以及向量数量积的坐标运算.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | -$\frac{2}{5}$ | D. | -$\frac{1}{5}$ |
| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | ($\frac{2}{3}$,$\frac{3}{2}$) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{3}{2}$,2) |
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
 已知抛物线y2=2px(p>0),点E(2,1),若斜率为2的弦过点E,且以E为弦中点.
已知抛物线y2=2px(p>0),点E(2,1),若斜率为2的弦过点E,且以E为弦中点.