题目内容
8．在△ABC中，∠ACB=90°，CD⊥AB于点D，AD：BD=2：3，则△ACD与△CBD的相似比为$\frac{\sqrt{6}}{3}$．分析 分别根据直角三角形的性质和相似三角形的性质直接解答即可．
解答 解：∵AD：BD=2：3，
∴设AD=2x，BD=3x，则AB=5x．
∵△ABC中，∠ACB=90°，CD⊥AB于点D
∴△BCD∽△BAC
∴$\frac{AB}{BC}=\frac{BC}{DB}$，
∴BC2=BD•AB=15x2，
∴在直角△ABC中，由勾股定理得到：AC2=AB2-BC2=10x2．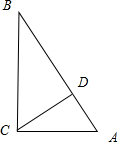
又∵△ACD∽△CBD，
∴（$\frac{AC}{BC}$）2=$\frac{10{x}^{2}}{15{x}^{2}}$=$\frac{2}{3}$，
则该相似三角形的相似比是：$\frac{AC}{BC}$=$\frac{\sqrt{6}}{3}$．
故答案是：$\frac{\sqrt{6}}{3}$．
点评 本题考查的是相似三角形的判定与性质，解此题的关键是要知道直角三角形斜边上的高把这个三角形分得的两个小三角形，与原三角形相似．
练习册系列答案
相关题目
如图，AB是圆柱OO′的一条母线，BC过底面圆心O，D是圆O上一点．已知AB=BC=10，S侧=2πrh=100π．
19．100辆汽车通过某一段公路时，时速的频率分布直方图如图所示，则时速在[50，70）的汽车大约有（ ）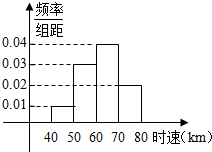
| A． | 60辆 | B． | 80辆 | C． | 70辆 | D． | 140辆 |
如图，在直角梯形ABCD中，AB∥CD，∠BAD=90°，且AB=AD=$\frac{1}{2}$CD=2，$\overrightarrow{CB}$=3$\overrightarrow{CM}$，则$\overrightarrow{DM}$•$\overrightarrow{AC}$的值为12．
3．下列命题中，正确的是（ ）
| A． | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$=$\overrightarrow{b}$ | B． | |$\overrightarrow{a}$|＞|$\overrightarrow{b}$|⇒$\overrightarrow{a}$＞$\overrightarrow{b}$ | C． | |$\overrightarrow{a}$|=|$\overrightarrow{b}$|⇒$\overrightarrow{a}$∥$\overrightarrow{b}$ | D． | |$\overrightarrow{a}$|=0⇒$\overrightarrow{a}$=$\overrightarrow{0}$ |