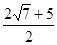题目内容
抛物线 的焦点为F,倾斜角为
的焦点为F,倾斜角为 的直线
的直线 过点F且与抛物线的一个交点为A,
过点F且与抛物线的一个交点为A, ,则抛物线的方程为
,则抛物线的方程为
A. | B. |
C. 或 或 | D. 或 或 |
D
解析试题分析:过A作AB⊥x轴于B点,则Rt△ABF中,∠AFB=60°,|AF|=3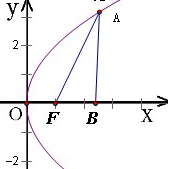
∴|BF|=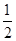 |AF|=
|AF|=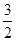 ,|AB|=
,|AB|=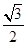 |AF|=
|AF|=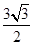 ,
,
设A的坐标为(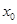 ,
,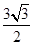 )
)
得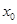 +
+ =3,且
=3,且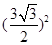 =2p
=2p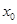 ,解之得p=
,解之得p=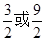
∴抛物线的方程为 或
或
故选D。
考点:本题主要考查抛物线的标准方程,抛物线的几何性质。
点评:中档题,求抛物线标准方程,往往利用定义或待定系数法。解答本题可利用结合选项验证的方法,如果A选项正确,则进一步验证 是否符合,如果B选项适合,则进一步验证
是否符合,如果B选项适合,则进一步验证 是否符合。
是否符合。

练习册系列答案
相关题目
已知动点 到两定点
到两定点 、
、 的距离和为8,且
的距离和为8,且 ,线段
,线段 的的中点为
的的中点为 ,过点
,过点 的所有直线与点
的所有直线与点 的轨迹相交而形成的线段中,长度为整数的有
的轨迹相交而形成的线段中,长度为整数的有
A. 条 条 | B. 条 条 | C. 条 条 | D. 条 条 |
已知 为双曲线C:
为双曲线C: 的左、右焦点,点
的左、右焦点,点 在
在 上,
上, ,则P到
,则P到 轴的距离为 ( )
轴的距离为 ( )
A. | B. | C. | D. |
已知 是以
是以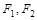 为焦点的椭圆
为焦点的椭圆 上的一点,若
上的一点,若
 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A. | B. | C. | D. |
双曲线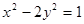 的右焦点的坐标为 ( )
的右焦点的坐标为 ( )
A.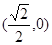 | B.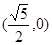 | C.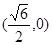 | D.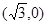 |
过抛物线 的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则
的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为3,则 等于( )
等于( )
| A.10 | B.8 | C.6 | D.4 |
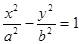 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x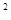 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ). 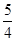
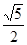
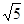
 轴上的双曲线的离心率为
轴上的双曲线的离心率为 ,则它的渐近线方程为( )
,则它的渐近线方程为( )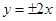
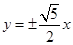
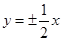
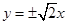
 中,
中, 为椭圆
为椭圆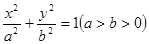 的四个顶点,F为其右焦点,直线
的四个顶点,F为其右焦点,直线 与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为
与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为