题目内容
已知
是以
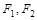为焦点的椭圆
上的一点，若
，则此椭圆的离心率为（ ）
A． | B． | C． | D． |
D
解析试题分析：设|PF1|=m，根据△PF1F2为直角三角形和tan∠PF1F2=-
，可分别表示出|PF2|和|F1F2|，进而表示出a和c，最后根据e=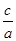
求得答案．
题得△PF1F2为直角三角形，设|PF1|=m，
则
∴
，
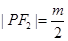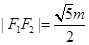
∴e=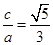
故选D．
考点：抛物线的简单性质
点评：本题考查椭圆离心率的求法．属基础题．
练习册系列答案
相关题目
：抛物线
的准线方程为
；命题
：平面内两条直线的斜率相等是两条直线平行的充分不必要条件；则下列命题是真命题的是（ ）
双曲线
的虚轴长是实轴长的2倍,则
（ ）
A． | B． | C． | D． |
设定点M（3，
）与抛物线
＝2x上的点P的距离为
，P到抛物线准线l的距为
，则＋取最小值时，P点的坐标为
| A．（0，0） | B．（1， ） | C．（2，2） | D．（ ，－ ） |
已知函数
与函数
，若
与
的交点在直线
的两侧，则实数
的取值范围是（ ）
A． | B． | C． | D． |
抛物线
的焦点为F，倾斜角为
的直线
过点F且与抛物线的一个交点为A，
，则抛物线的方程为
A． | B． |
C． 或 | D．或 |
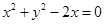若曲线
：
与曲线
：
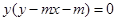有四个不同的交点，则实数m的取值范围是（ ）
A．( ， ) | B．(，0)∪(0，) |
| C．[，] | D．( ，)∪(，+ ) |
设
是椭圆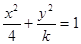
的离心率，且
，则实数
的取值范围是（ ）
| A． (0，3) | B． (3， ) |
C． (0，3) ( ,+ ) | D． (0，2) |
抛物线y2=2Px，过点A（2，4），F为焦点，定点B的坐标为（8，-8），则|AF|∶|BF|值为
| A．1∶4 | B．1∶2 | C．2∶5 | D．3∶8 |