题目内容
18.求曲线f(x)=$\frac{{e}^{x}}{x}$在点(1,f(1))处的切线方程.分析 先求出导函数,然后利用导数的几何意义求出切线斜率k=y′|x=1,利用点斜式即可写出切线方程
解答 解:∵y=f(x)=$\frac{{e}^{x}}{x}$,
∴y′=f′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$,
则切线斜率k=y′|x=1=0,
∴在点(1,e)处的切线方程为:y-e=0(x-1),
即y=e.
点评 本题考查利用导数研究曲线上某点切线方程,考查直线方程的求法,考查导数的几何意义,属基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
3.过抛物线y2=8x的焦点作圆(x-1)2+y2=4的弦,其中最短的弦长为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
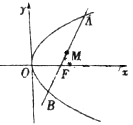 如图,已知抛物线y2=2px(p>0)的焦点为F,过F的直线交抛物线于A、B两点.
如图,已知抛物线y2=2px(p>0)的焦点为F,过F的直线交抛物线于A、B两点.