题目内容
一机器可以按各种不同速度运转,其生产的产品有一些会有缺点,每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据:
| 速度(x转/秒) |
| ||
| 8 | 6 | ||
| 9 | 8 | ||
| 10 | 10 | ||
| 13 | 12 |
(2)、求机器运转速度与每小时生产有缺点的产品数之间的回归方程;(系数
 用分数表示)
用分数表示)(3)、若实际生产所允许的每小时生产有缺点的产品数不超过10件,那么机器的速度每秒不超过多少转?
(1)散点图如下: ……5分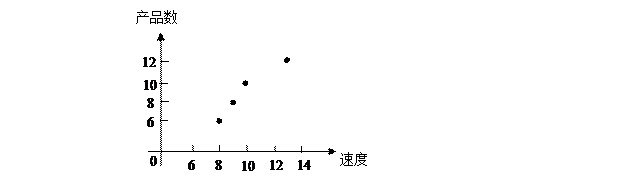
(2)∵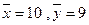 ,
,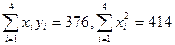
∴回归系数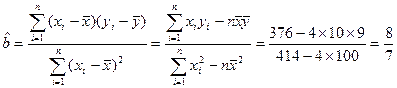 ……7分
……7分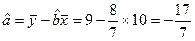 ……9分
……9分
∴回归直线方程为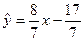 ……10分
……10分
(3)若实际生产所允许的每小时生产有缺点的产品数不超过10件,则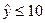
即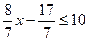 解得
解得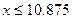 ……13分
……13分
∴实际生产所允许的每小时生产有缺点的产品数不超过10件,那么机器的速度应每秒不超过10.875转 ……14分
解析

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
(13分)
某研究机构为了研究人的脚的大小(码)与身高(厘米)之间的关系,随机抽测了20人,得到如下数据:
| 序号 | 身高x | 脚长y | 序号 | 身高x | 脚长y |
| 1 | 176 | 42 | 11 | 179 | 44 |
| 2 | 175 | 44 | 12 | 169 | 43 |
| 3 | 174 | 41 | 13 | 185 | 45 |
| 4 | 180 | 44 | 14 | 166 | 40 |
| 5 | 170 | 42 | 15 | 174 | 42 |
| 6 | 178 | 43 | 16 | 167 | 42 |
| 7 | 173 | 42 | 17 | 173 | 41 |
| 8 | 168 | 40 | 18 | 174 | 42 |
| 9 | 190 | 46 | 19 | 172 | 42 |
| 10 | 171 | 42 | 20 | 175 | 41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”,“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成如下2×2列联表;
| | 高个 | 非高个 | 合计 |
| 大脚 | | | |
| 非大脚 | | 12 | |
| 合计 | | | 20 |
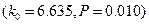
(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
| 分组 | 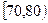 | 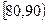 | 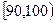 |  | 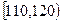 | 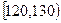 | 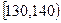 | [140,150] |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | 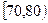 | 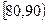 | 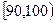 |  | 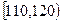 | 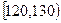 | 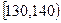 | [140,150] |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
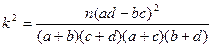
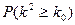 | 0.10 | 0.025 | 0.010 |
 | 2.706 | 5.024 | 6.635 |
17.有甲乙两个班级进行数学考 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10[来源:学科网ZXXK] | | |
| 乙班 | | 30 | [来源:学#科#网] |
| 合计 | | | 105 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成
 绩与班级有关系”。
绩与班级有关系”。(3)若按下面的方法从甲班优秀的学生抽取一人;把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取的人的序号,试求抽到6或10的概率。
已知x与y之间的一组数据
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
(2)若
 x与y线性相关,写出线性回归方程必定经过的点
x与y线性相关,写出线性回归方程必定经过的点(3)若x与y线性相关求出线性回归方程,
(4)说出2个刻画回归效果的手段,假设R
 =0.74
=0.74 说明什么问题。
说明什么问题。参考公式
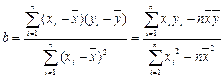
 依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.
依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.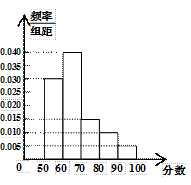
 级的
级的 名学生参加一次科普知识竞赛,然后随机抽取
名学生参加一次科普知识竞赛,然后随机抽取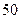 名学生的成绩进行统计分析.
名学生的成绩进行统计分析.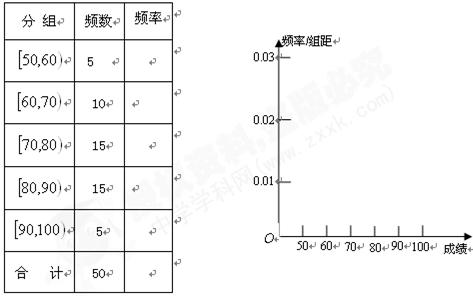
 表示抽取的3名学生中男学生数,求
表示抽取的3名学生中男学生数,求
 ,
, ,
,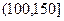 ,
,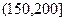 ,
,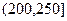 ,
,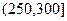 进行分组,得到频率分布直方图如图.
进行分组,得到频率分布直方图如图.  的值;
的值;