题目内容
(本小题满分12分)
甲乙两个学校高三年级分别为1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在[120,150]内为优秀)
甲校:
| 分组 | 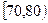 | 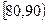 | 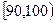 |  | 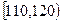 | 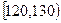 | 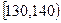 | [140,150] |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | 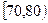 | 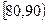 | 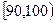 |  | 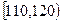 | 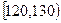 | 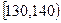 | [140,150] |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(2)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
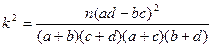
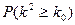 | 0.10 | 0.025 | 0.010 |
 | 2.706 | 5.024 | 6.635 |
解:(1)依题甲校抽取55人,乙校抽取50分, …………2分
故x=6,y="7 " …………4分
估计甲校优秀率为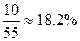
乙校优秀率为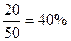 …………6分
…………6分
(2)
…………8分 甲校 乙校 总计 优秀 10 20 
30 非优秀 45 30 75 总计 55 50 105 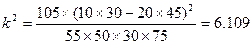 …………10分
…………10分
又因为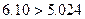 …………11分
…………11分
故有97.5%的把握认为两个学校的数学成绩有差异. …………12分
(注:未经过计算,或计算错误答出有97.5%的把握认为两个学校的数学成绩有差异的同学不得分.)
解析

 每课必练系列答案
每课必练系列答案一机器可以按各种不同速度运转,其生产的产品有一些会有缺点,每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据:
| 速度(x转/秒) |
| ||
| 8 | 6 | ||
| 9 | 8 | ||
| 10 | 10 | ||
| 13 | 12 |
(2)、求机器运转速度与每小时生产有缺点的产品数之间的回归方程;(系数
 用分数表示)
用分数表示)(3)、若实际生产所允许的每小时生产有缺点的产品数不超过10件,那么机器的速度每秒不超过多少转?
.已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| | 甲 | 乙 | 丙 |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(Ⅱ)确定x,y,z的值,使成本最低.
(本题10分) 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整 数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
 60.5~70.5 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 50 | |
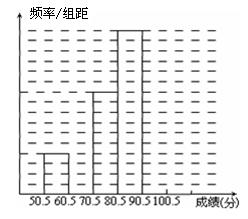
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)

 补全频率分布直方图;
补全频率分布直方图;(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,
问该校获得二等奖的学生约为多少人?
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2) 请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
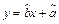 ;
;(附:最小二乘法求线性回归方程系数公式
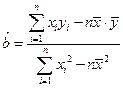 ,
,
另外:计算数据3×2.5+4×3+5×4+6×4.5=66.5可供使用)
(3) 已知该厂技术改造前100吨甲产品能耗为90吨标准煤;试根据(2)所求出的线性回归方程,预测生产
 100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
100吨甲产品的生产能耗比技术改造前降低多少吨标准煤? 


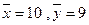
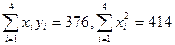
 万元与公司所获得利润
万元与公司所获得利润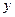 万元之间有如下的统计数据:
万元之间有如下的统计数据: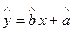 ;
;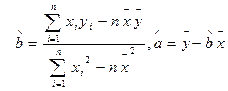
 止投篮测试的概率是多少?
止投篮测试的概率是多少?