题目内容
【题目】已知三棱锥M-ABC中,MA=MB=MC=AC=![]() ,AB=BC=2,O为AC的中点,点N在边BC上,且
,AB=BC=2,O为AC的中点,点N在边BC上,且![]() .
.
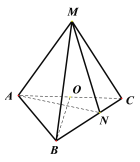
(1)证明:BO![]() 平面AMC;
平面AMC;
(2)求二面角N-AM-C的正弦值.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)先证明![]() ,
,![]() 即可证明BO
即可证明BO![]() 平面AMC;
平面AMC;
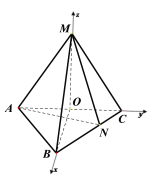
(2)因为![]() 两两垂直,建立空间直角坐标系
两两垂直,建立空间直角坐标系![]() 如图所示.求出平面
如图所示.求出平面![]() 与平面
与平面![]() 的法向量,代入公式即可得到结果.
的法向量,代入公式即可得到结果.
(1)如图所示:连接![]() ,
,
在![]() 中:
中:![]() ,则
,则![]() ,
,![]() .
.
在![]() 中:
中:![]() ,
,![]() 为
为![]() 的中点,则
的中点,则![]() ,且
,且![]()
在![]() 中:
中:![]() ,满足:
,满足:![]()
根据勾股定理逆定理得到![]()
![]() 相交于
相交于![]() ,
,
故![]() 平面
平面![]() .
.
(2)因为![]() 两两垂直,建立空间直角坐标系
两两垂直,建立空间直角坐标系![]() 如图所示.因为
如图所示.因为![]() ,
,![]() ,
,
则![]() ,
,
由![]() 所以,
所以,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
令![]() ,得
,得![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的法向量,
的法向量,
所以![]() 与
与![]() 所成角的余弦为
所成角的余弦为![]() .
.
所以二面角的正弦值为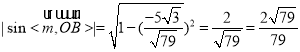

 阅读快车系列答案
阅读快车系列答案【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得数据如下表(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(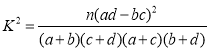 ,其中
,其中 ![]() )
)
抗倒伏数据如下:
143 147 147 151 153 153 157 159 160 164 166 169 174 175 175
180 188 188 192 195 195 199 203 206 206
易倒伏数据如下:
151 167 175 178 181 182 186 186 187 190 190 193 194 195 198
199 199 202 202 203
(1)完成 2×2 列联表,并说明能否在犯错概率不超过0.01的条件下认为抗倒伏是否与玉米矮茎有关?
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,再从这9株中取出两株进行杂交试验,设取出的易倒伏玉米株数为X,求X的分布列(概率用组合数算式表示);
(ii)若将频率视为概率,从抗倒伏的玉米试验田中再随机取出50株,求取出的高茎玉米株数的数学期望和方差.
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98,请估计该等级的中国小龙虾销售单价为多少元?
参考公式:对一组数据![]() ,
,![]() ,····
,····![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: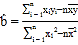 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】某种植物感染![]() 病毒极易导致死亡,某生物研究所为此推出了一种抗
病毒极易导致死亡,某生物研究所为此推出了一种抗![]() 病毒的制剂,现对20株感染了
病毒的制剂,现对20株感染了![]() 病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:mg)进行统计.规定:植株吸收在6mg(包括6mg)以上为“足量”,否则为“不足量”.现对该20株植株样本进行统计,其中 “植株存活”的13株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量(mg) | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
(1)完成以下![]() 列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为“植株的存活”与“制剂吸收足量”有关?
吸收足量 | 吸收不足量 | 合计 | |
植株存活 | 1 | ||
植株死亡 | |||
合计 | 20 |
(2)①若在该样本“吸收不足量”的植株中随机抽取3株,记![]() 为“植株死亡”的数量,求
为“植株死亡”的数量,求![]() 得分布列和期望
得分布列和期望![]() ;
;
②将频率视为概率,现在对已知某块种植了1000株并感染了![]() 病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量
病毒的该植物试验田里进行该药品喷雾试验,设“植株存活”且“吸收足量”的数量为随机变量![]() ,求
,求![]() .
.
参考数据: ,其中
,其中![]()