题目内容
【题目】![]() 为固定的整数,定义任意整数坐标点
为固定的整数,定义任意整数坐标点![]() 关于
关于![]() 的余数是
的余数是![]() 关于
关于![]() 的余数.找出所有正整数数组
的余数.找出所有正整数数组![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的长方形具有如下性质:
为顶点的长方形具有如下性质:
ⅰ.长方形内整数点以![]() 为余数出现的次数相同;
为余数出现的次数相同;
ⅱ.长方形边界上整数点以![]() 为余数出现的次数相同.
为余数出现的次数相同.
【答案】满足条件的![]() 为:当
为:当![]() 时,
时,![]() 中至少有一个为奇数;当
中至少有一个为奇数;当![]() 时,
时,![]()
![]() 或
或![]()
【解析】
长方形边界上共有![]() 个整点,则有
个整点,则有![]() .
.
长方形内共有![]() 个整点,则有
个整点,则有![]() .
.
当![]() 时,为使其中被2除余0,1的点的个数相同,则必有
时,为使其中被2除余0,1的点的个数相同,则必有![]() .
.
从而,![]() 中至少有一个为奇数.
中至少有一个为奇数.
另一方面,当![]() 中至少有一个为奇数时,不妨设
中至少有一个为奇数时,不妨设![]() 为奇数,则对一切
为奇数,则对一切![]() 在
在![]() 个点
个点![]() 中被2除余0,1的点的个数相同.从而,长方形内的整点中被2除余0,1的个数相同.
中被2除余0,1的点的个数相同.从而,长方形内的整点中被2除余0,1的个数相同.
又![]() 及
及![]() 中被2除余0,1的点的个数相同,且对一切
中被2除余0,1的点的个数相同,且对一切![]() ,点
,点![]() 与
与![]() 被2除余数一个为0,一个为1.从而,长方形边界上的点中被2除余0,1的个数也相同.
被2除余数一个为0,一个为1.从而,长方形边界上的点中被2除余0,1的个数也相同.
故此时![]() 满足要求,其中
满足要求,其中![]() 中至少有一个奇数.
中至少有一个奇数.
当![]() 时,边界上共有
时,边界上共有![]() 个整点:
个整点:
![]() 与
与
![]() .
.
它们的坐标和分别为![]() 与
与![]() .
.
设![]() 则边界上的点中被
则边界上的点中被![]() 除余
除余![]() 的有偶数个,
的有偶数个,
且若![]() ,则边界上的点中被
,则边界上的点中被![]() 除余0的有奇数个, 这不可能,故必有
除余0的有奇数个, 这不可能,故必有![]() .
.
且当![]() 时, 边界上的点中被
时, 边界上的点中被![]() 除余
除余![]() 的个数必相同.
的个数必相同.
又长方形内部共有![]() 个点,故必有
个点,故必有![]() .
.
若![]() ,则设
,则设![]() 分别是
分别是![]() 除以
除以![]() 的余数,
的余数,
则![]() ,且若
,且若![]() ,则又由
,则又由![]() 知
知![]() ,从而,
,从而,
![]() .
.
这不可能,故![]() .同理知
.同理知![]() .
.
于是,长方形内部整点被![]() 除余
除余![]() 的个数相同等价于
的个数相同等价于![]()
![]() 中被
中被![]() 除余
除余![]() 的个数相同.
的个数相同.
又![]() ,故必有
,故必有![]() .于是,
.于是,
![]() 中没有被
中没有被![]() 除余0的点,矛盾.
除余0的点,矛盾.
从而![]() 之一必被
之一必被![]() 除余1,而另一个被
除余1,而另一个被![]() 除余
除余![]() .此时,由于
.此时,由于![]() 或
或![]() ,可知内部整点被
,可知内部整点被![]() 除余
除余![]() 的个数相同.
的个数相同.
综上所述,满足条件的![]() 为:当
为:当![]() 时,
时,![]() 中至少有一个为奇数;当
中至少有一个为奇数;当![]() 时,
时,![]()
![]() 或
或![]() .
.

【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测
,并预测![]() 地区2019年足球特色学校的个数(精确到个).
地区2019年足球特色学校的个数(精确到个).
本题参考公式和数据: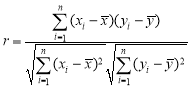 ,
,![]() ,
,![]() ,
,![]() ,
,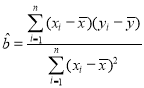 ,
,![]() .
.