题目内容
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得数据如下表(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(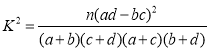 ,其中
,其中 ![]() )
)
抗倒伏数据如下:
143 147 147 151 153 153 157 159 160 164 166 169 174 175 175
180 188 188 192 195 195 199 203 206 206
易倒伏数据如下:
151 167 175 178 181 182 186 186 187 190 190 193 194 195 198
199 199 202 202 203
(1)完成 2×2 列联表,并说明能否在犯错概率不超过0.01的条件下认为抗倒伏是否与玉米矮茎有关?
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,再从这9株中取出两株进行杂交试验,设取出的易倒伏玉米株数为X,求X的分布列(概率用组合数算式表示);
(ii)若将频率视为概率,从抗倒伏的玉米试验田中再随机取出50株,求取出的高茎玉米株数的数学期望和方差.
【答案】(1)列联表见解析,能在犯错概率不超过0.01的条件下认为抗倒伏是否与玉米矮茎有关;(2)(i)见解析;(ii)期望为![]() ,方差为
,方差为![]()
【解析】
(1)根据题意得出2×2 列联表,根据公式计算出![]() 即可得解;
即可得解;
(2)(i)根据分层抽样得易倒伏4株,抗倒伏5株,分别计算概率即可得到分布列;
(ii)利用二项分布求解期望和方差.
(1)根据统计数据可得2×2 列联表,
抗倒伏 | 易倒伏 | 合计 | |
矮茎 | 15 | 4 | 19 |
高茎 | 10 | 16 | 26 |
合计 | 25 | 20 | 45 |
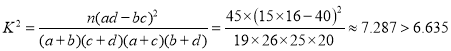
所以能在犯错概率不超过0.01的条件下认为抗倒伏是否与玉米矮茎有关;
(2)(i)按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽出9株玉米,
则易倒伏4株,抗倒伏5株,从这9株中取出两株进行杂交试验,设取出的易倒伏玉米株数为X,则X所有可能的取值为0,1,2,
![]()
X的分布列如下:
P | 0 | 1 | 2 |
X |
|
|
(ii)若将频率视为概率,从抗倒伏的玉米中取出的高茎玉米概率为![]()
从抗倒伏的玉米试验田中再随机取出50株,记取出的高茎玉米株数为随机变量Y,
则![]()
Y的数学期望和方差分别为![]()

【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测
,并预测![]() 地区2019年足球特色学校的个数(精确到个).
地区2019年足球特色学校的个数(精确到个).
本题参考公式和数据: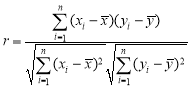 ,
,![]() ,
,![]() ,
,![]() ,
,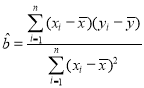 ,
,![]() .
.