题目内容
已知椭圆 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C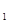 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切.
(Ⅰ)已知椭圆 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C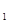 的方程.
的方程.
 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C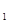 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切.(Ⅰ)已知椭圆
 的离心率;
的离心率;(Ⅱ)若
 的最大值为49,求椭圆C
的最大值为49,求椭圆C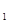 的方程.
的方程.(Ⅰ)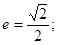 (Ⅱ)
(Ⅱ) .
.
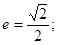 (Ⅱ)
(Ⅱ) .
.(I)先求出直线l的方程为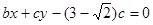 ,然后根据因为直线与圆
,然后根据因为直线与圆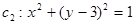 相切,得到
相切,得到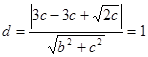 ,从而可得到a,c的关系,进而求出e.
,从而可得到a,c的关系,进而求出e.
(II) 在(I)的基础上,可把椭圆方程转化为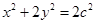 ,这样根据条件建立关于c的方程即可求出椭圆方程,因而设
,这样根据条件建立关于c的方程即可求出椭圆方程,因而设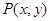 、圆
、圆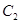 的圆心记为
的圆心记为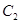 ,则
,则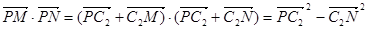
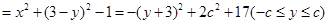 ,根据其最大值为49,可求出c的值.
,根据其最大值为49,可求出c的值.
(Ⅰ)由题意可知直线l的方程为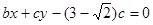 ,
,
因为直线与圆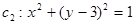 相切,所以
相切,所以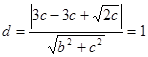 ,即
,即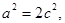
从而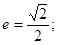 …………………5分
…………………5分
(Ⅱ)设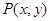 、圆
、圆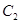 的圆心记为
的圆心记为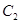 ,则
,则
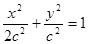 (
(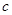 ﹥0),又
﹥0),又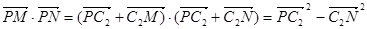 =
=
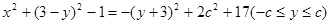 . …………………8分
. …………………8分
j当
 ;
;
k当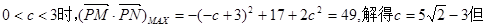
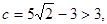 故舍去.
故舍去.
综上所述,椭圆的方程为 . …………………12分
. …………………12分
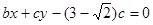 ,然后根据因为直线与圆
,然后根据因为直线与圆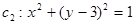 相切,得到
相切,得到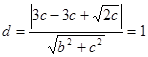 ,从而可得到a,c的关系,进而求出e.
,从而可得到a,c的关系,进而求出e.(II) 在(I)的基础上,可把椭圆方程转化为
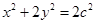 ,这样根据条件建立关于c的方程即可求出椭圆方程,因而设
,这样根据条件建立关于c的方程即可求出椭圆方程,因而设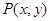 、圆
、圆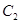 的圆心记为
的圆心记为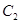 ,则
,则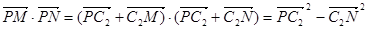
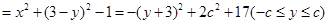 ,根据其最大值为49,可求出c的值.
,根据其最大值为49,可求出c的值.(Ⅰ)由题意可知直线l的方程为
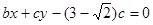 ,
,因为直线与圆
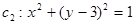 相切,所以
相切,所以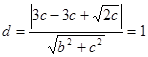 ,即
,即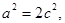
从而
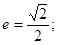 …………………5分
…………………5分(Ⅱ)设
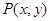 、圆
、圆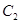 的圆心记为
的圆心记为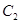 ,则
,则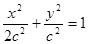 (
(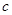 ﹥0),又
﹥0),又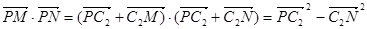 =
=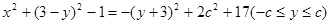 . …………………8分
. …………………8分j当

 ;
;k当
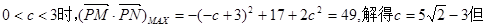
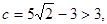 故舍去.
故舍去.综上所述,椭圆的方程为
 . …………………12分
. …………………12分
练习册系列答案
相关题目
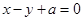 与圆
与圆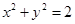 相切,则
相切,则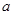 的值为 ( )
的值为 ( ) 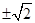
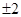
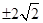
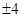
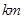 的圆形村落,
的圆形村落,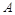 、
、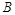 两人同时从村落中心出发。
两人同时从村落中心出发。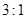 ,且后来
,且后来
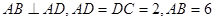 ,动点P在以点C为圆心且与直线BD相切的圆上运动,设
,动点P在以点C为圆心且与直线BD相切的圆上运动,设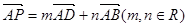 ,则
,则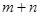 的取值范围是 。
的取值范围是 。 ,斜率
,斜率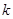 的直线
的直线 与椭圆相交于点
与椭圆相交于点 ,点
,点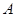 是线段
是线段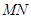 的中点,直线
的中点,直线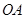 (
(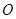 为坐标原点)的斜率是
为坐标原点)的斜率是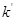 ,那么
,那么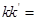
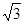 x-4的距离的最小值是 .
x-4的距离的最小值是 .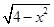 (|x|≤2)与直线y=k(x-2)+4有两个交点时,实数k的取值范围是( )
(|x|≤2)与直线y=k(x-2)+4有两个交点时,实数k的取值范围是( ) 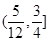
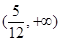
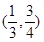

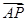 ·
·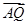 的值为______.
的值为______.