题目内容
(本题满分15分)
设有半径为3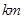 的圆形村落,
的圆形村落,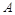 、
、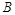 两人同时从村落中心出发。
两人同时从村落中心出发。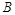 一直向北直行;
一直向北直行;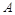 先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝
先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝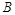 所在的方向前进。
所在的方向前进。
(1)若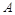 在距离中心5
在距离中心5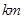 的地方改变方向,建立适当坐标系,
的地方改变方向,建立适当坐标系,
求: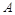 改变方向后前进路径所在直线的方程
改变方向后前进路径所在直线的方程
(2)设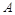 、
、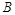 两人速度一定,其速度比为
两人速度一定,其速度比为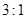 ,且后来
,且后来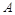 恰与
恰与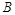 相遇.问两人在何处相遇?
相遇.问两人在何处相遇?
(以村落中心为参照,说明方位和距离)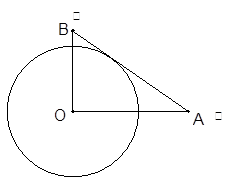
设有半径为3
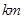 的圆形村落,
的圆形村落,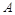 、
、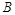 两人同时从村落中心出发。
两人同时从村落中心出发。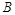 一直向北直行;
一直向北直行;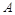 先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝
先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝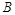 所在的方向前进。
所在的方向前进。(1)若
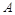 在距离中心5
在距离中心5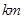 的地方改变方向,建立适当坐标系,
的地方改变方向,建立适当坐标系,求:
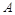 改变方向后前进路径所在直线的方程
改变方向后前进路径所在直线的方程(2)设
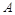 、
、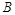 两人速度一定,其速度比为
两人速度一定,其速度比为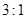 ,且后来
,且后来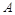 恰与
恰与 相遇.问两人在何处相遇?
相遇.问两人在何处相遇?(以村落中心为参照,说明方位和距离)
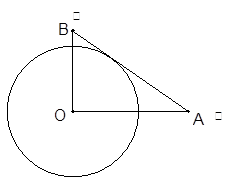
(1) 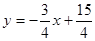 ;(2) A、B相遇点在村落中心正北距离
;(2) A、B相遇点在村落中心正北距离 千米处
千米处
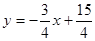 ;(2) A、B相遇点在村落中心正北距离
;(2) A、B相遇点在村落中心正北距离 千米处
千米处本题考查了圆的方程的综合应用,在这个题中注意解决实际问题的基本步骤,及题目条件的转化,体现了转化思想和数形结合思想,是个中档题.
(1)建立如图坐标系:得到点的坐标,进而求解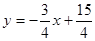
(2)先根据题意,以村落中心为坐标原点,向东的方向为x轴建立直角坐标系,根据两人的速度关系设其速度及各点,将实际问题转化为数学问题,利用图形中的直角三角形得到5x0=4y0,代入直线的斜率公式可得直线的斜率,再利用直线与圆相切即可的直线方程,也就得到了该问题的解.
(1)建立如图坐标系: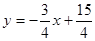
(2)由题意可设A、B两人速度分别为3v千米/小时 ,v千米/小时,
再设A出发x0小时,在点P改变方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0, 0),(0,vx0+vy0).

由|OP|2+|OQ|2=|PQ|2知,
(3vx0)2+(vx0+vy0)2=(3vy0)2,
即 .
.
 ……①
……①
将①代入
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线 相切,则有
相切,则有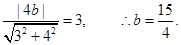
答:A、B相遇点在村落中心正北距离 千米处
千米处
(1)建立如图坐标系:得到点的坐标,进而求解
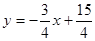
(2)先根据题意,以村落中心为坐标原点,向东的方向为x轴建立直角坐标系,根据两人的速度关系设其速度及各点,将实际问题转化为数学问题,利用图形中的直角三角形得到5x0=4y0,代入直线的斜率公式可得直线的斜率,再利用直线与圆相切即可的直线方程,也就得到了该问题的解.
(1)建立如图坐标系:
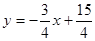
(2)由题意可设A、B两人速度分别为3v千米/小时 ,v千米/小时,
再设A出发x0小时,在点P改变方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0, 0),(0,vx0+vy0).

由|OP|2+|OQ|2=|PQ|2知,
(3vx0)2+(vx0+vy0)2=(3vy0)2,
即
 .
. ……①
……①将①代入

又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线
 相切,则有
相切,则有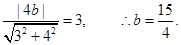
答:A、B相遇点在村落中心正北距离
 千米处
千米处
练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
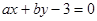 和圆
和圆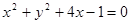 相切与点
相切与点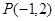 ,则
,则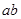 的值为( )
的值为( )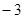
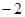
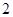
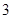
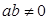 ,点
,点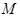
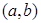 是圆
是圆 内一点,直线
内一点,直线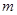 是以点
是以点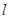 的方程是
的方程是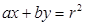 ,则下列结论正确的是( )
,则下列结论正确的是( )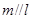 ,且
,且 ,且
,且 的位置关系是
的位置关系是 与圆
与圆 的位置关系是 ( )
的位置关系是 ( )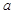 为任意实数时,直线
为任意实数时,直线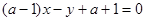 恒过定点
恒过定点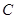 ,则以
,则以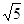 为半径的圆的方程是_____________.
为半径的圆的方程是_____________. 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的圆心
的圆心 轴上,半径为1,直线
轴上,半径为1,直线 ,被圆
,被圆 ,且圆心
,且圆心 的下方.
的下方. ,若圆
,若圆 的内切圆,求△
的内切圆,求△ 的最大值和最小值.
的最大值和最小值.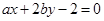
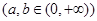 平分圆
平分圆 ,则
,则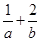 的最小值是
的最小值是