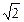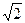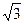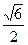题目内容
双曲线的中心在坐标原点,焦点F(2,0)到一条渐近线的距离为1,试求过F所作一渐近线的垂线l被双曲线截得的线段长.
设此双曲线方程为
=1(a>0,b>0),其渐近线方程为
±
=0
bx±ay=0,
d=1=
.
∴b=1,a=
.
∴双曲线方程为
-y2=1.
设其一条渐近线为y=-
x,过F(2,0)且与此渐近线垂直的直线l:y=-(x-2).
联立
8x2-36x+39=0
线段长=
|x1-x2|
=
·
=2·
.
=1(a>0,b>0),其渐近线方程为±=0bx±ay=0,d=1=
.∴b=1,a=
.∴双曲线方程为
-y2=1.设其一条渐近线为y=-
x,过F(2,0)且与此渐近线垂直的直线l:y=-(x-2).联立
8x2-36x+39=0线段长=
|x1-x2|=
·=2·
.
练习册系列答案
名校课堂系列答案
相关题目
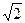,则双曲线方程为_____________.
-
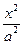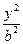=1,点A、B在双曲线的右支上，线段AB经过双曲线的右焦点F2，|AB|=m,F1为另一焦点，则△ABF1的周长为( )
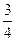x,则此双曲线的( )
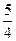或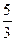
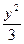=1的右焦点作直线与双曲线交于A、B两点,若OA⊥OB(O为坐标原点),求AB所在直线的方程.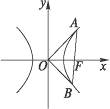
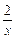的图象是平面上到两定点距离之差的绝对值等于定长的点的轨迹,则这两个定点间的距离为
