题目内容
如图所示,过双曲线x2-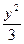 =1的右焦点作直线与双曲线交于A、B两点,若OA⊥OB(O为坐标原点),求AB所在直线的方程.
=1的右焦点作直线与双曲线交于A、B两点,若OA⊥OB(O为坐标原点),求AB所在直线的方程.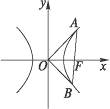
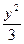 =1的右焦点作直线与双曲线交于A、B两点,若OA⊥OB(O为坐标原点),求AB所在直线的方程.
=1的右焦点作直线与双曲线交于A、B两点,若OA⊥OB(O为坐标原点),求AB所在直线的方程.
直线方程为y=± (x-2).
(x-2).
 (x-2).
(x-2).设A、B两点的坐标分别为(x1,y1)、(x2,y2),双曲线x2-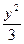 =1的右焦点为F(2,0),因此,直线AB过点(2,0),当直线AB垂直于x轴时,把x1=x2=2代入双曲线方程,得y1=3,y2=-3,此时OA不垂直于OB,不合题意;当AB不垂直于x轴时,设其斜率为k,方程为y=k(x-2),代入双曲线方程,整理得(3-k2)x2+4k2x-4k2-3=0,∴x1x2=
=1的右焦点为F(2,0),因此,直线AB过点(2,0),当直线AB垂直于x轴时,把x1=x2=2代入双曲线方程,得y1=3,y2=-3,此时OA不垂直于OB,不合题意;当AB不垂直于x轴时,设其斜率为k,方程为y=k(x-2),代入双曲线方程,整理得(3-k2)x2+4k2x-4k2-3=0,∴x1x2=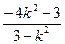 ,x1+x2=
,x1+x2=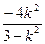 . ①
. ①
∴y1y2=k(x1-2)·k(x2-2)=k2[x1x2-2(x1+x2)+4].∵OA⊥OB,∴ =-1(显然x1≠0,x2≠0),
=-1(显然x1≠0,x2≠0),
即x1x2+y1y2=0.∴x1x2+k2[x1x2-2(x1+x2)+4]=0,把①式代入得(k2+1)·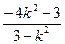 -2k2·
-2k2·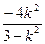 +4k2=0,
+4k2=0,
解得k2= ,k=±
,k=± ,因此,所求直线方程为y=±
,因此,所求直线方程为y=± (x-2).
(x-2).
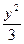 =1的右焦点为F(2,0),因此,直线AB过点(2,0),当直线AB垂直于x轴时,把x1=x2=2代入双曲线方程,得y1=3,y2=-3,此时OA不垂直于OB,不合题意;当AB不垂直于x轴时,设其斜率为k,方程为y=k(x-2),代入双曲线方程,整理得(3-k2)x2+4k2x-4k2-3=0,∴x1x2=
=1的右焦点为F(2,0),因此,直线AB过点(2,0),当直线AB垂直于x轴时,把x1=x2=2代入双曲线方程,得y1=3,y2=-3,此时OA不垂直于OB,不合题意;当AB不垂直于x轴时,设其斜率为k,方程为y=k(x-2),代入双曲线方程,整理得(3-k2)x2+4k2x-4k2-3=0,∴x1x2=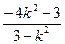 ,x1+x2=
,x1+x2=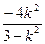 . ①
. ①∴y1y2=k(x1-2)·k(x2-2)=k2[x1x2-2(x1+x2)+4].∵OA⊥OB,∴
 =-1(显然x1≠0,x2≠0),
=-1(显然x1≠0,x2≠0),即x1x2+y1y2=0.∴x1x2+k2[x1x2-2(x1+x2)+4]=0,把①式代入得(k2+1)·
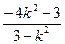 -2k2·
-2k2·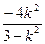 +4k2=0,
+4k2=0,解得k2=
 ,k=±
,k=± ,因此,所求直线方程为y=±
,因此,所求直线方程为y=± (x-2).
(x-2).
练习册系列答案
相关题目
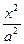 -
-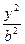 =1(a>0,b>0)满足如下条件:①ab=
=1(a>0,b>0)满足如下条件:①ab=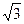 ;②直线l过右焦点F,斜率为
;②直线l过右焦点F,斜率为 ,交y轴于点P,线段PF交H于Q,且|PQ|∶|QF|=2∶1.求双曲线的方程.
,交y轴于点P,线段PF交H于Q,且|PQ|∶|QF|=2∶1.求双曲线的方程.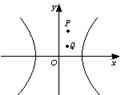
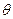 ∈(0,
∈(0,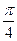 ),则二次曲线x
),则二次曲线x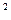 cos
cos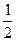 )
)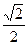 )
)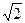 )
)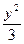 =1,过(2,0)的直线被双曲线截得长为6的直线有___________条.
=1,过(2,0)的直线被双曲线截得长为6的直线有___________条.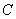 的方程为
的方程为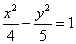 ,若直线
,若直线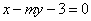 截双曲线的一支所得弦长为5
截双曲线的一支所得弦长为5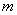 的值;
的值;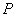 的直线与双曲线的两条渐近线分别交于
的直线与双曲线的两条渐近线分别交于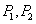 ,且点
,且点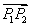 所成的比为
所成的比为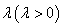 。当
。当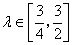 时,求
时,求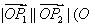 为坐标原点)的最大值和最小值
为坐标原点)的最大值和最小值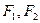 是双曲线
是双曲线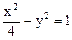 的两个焦点,P在双曲线上,
的两个焦点,P在双曲线上,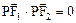 ,则
,则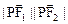 的值等于___________。
的值等于___________。