题目内容
【题目】已知椭圆M的对称轴为坐标轴,离心率为![]() ,且一个焦点坐标为(
,且一个焦点坐标为(![]() ,0).
,0).
(1)求椭圆M的方程;
(2)设直线l与椭圆M相交于A,B两点,以线段OA,OB为邻边作平行四边形OAPB,其中点P在椭圆M上,O为坐标原点,求点O到直线l的距离的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设椭圆的标准方程,已知离心率e=![]() ,一个焦点(c,0)=(
,一个焦点(c,0)=(![]() ,0),结合a2=b2+c2,求得a,b,c的值,即可得椭圆方程;
,0),结合a2=b2+c2,求得a,b,c的值,即可得椭圆方程;
(2)分类讨论,当直线l的斜率存在时,得O到l的最小值为![]() ,当直线l的斜率不存在时,得最小值为1,综合考虑,可知点O到l的最小值是
,当直线l的斜率不存在时,得最小值为1,综合考虑,可知点O到l的最小值是![]() .
.
(1)由题意可设椭圆的标准方程为![]() =1(a>b>0),∴
=1(a>b>0),∴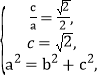 解得a=2,b=
解得a=2,b=![]() ,
,
∴ 椭圆M的方程为![]() =1.
=1.
当直线l的斜率存在时,设直线l的方程为y=kx+m,联立![]()
化为(1+2k2)x2+4kmx+2m2-4=0
,Δ=16k2m2-4(1+2k2)(2m2-4)>0,化为2+4k2-m2>0,
设A(x1,y1),B(x2,y2),P(x0,y0).
∴x0=x1+x2=![]() ,y0=y1+y2=k(x1+x2)+2m=
,y0=y1+y2=k(x1+x2)+2m=![]() .
.
∵点P在椭圆M上,∴![]() =1.
=1.
∴![]() =1,化简得2m2=1+2k2,满足Δ>0.
=1,化简得2m2=1+2k2,满足Δ>0.
又点O到直线l的距离d=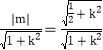 =
=![]() .
.
当且仅当k=0时取等号.
当直线l无斜率时,由对称性可知:点P一定在x轴上,从而点P的坐标为(±2,0),直线l的方程为x=±1,∴点O到直线l的距离为1.
∴点O到直线l的距离的最小值为![]() .
.

练习册系列答案
相关题目