题目内容
13.设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,且PA⊥l,A为垂足,如果直线AF的斜率为-1,则|PF|等于( )| A. | 2 | B. | 4 | C. | 8 | D. | 12 |
分析 先根据抛物线方程求出焦点坐标和准线方程,根据直线AF的斜率得到AF方程,与准线方程联立,解出A点坐标,因为PA垂直准线l,所以P点与A点纵坐标相同,再代入抛物线方程求P点横坐标,利用抛物线的定义就可求出|PF|长.
解答 解:∵抛物线方程为y2=8x,
∴焦点F(2,0),准线l方程为x=-2,
∵直线AF的斜率为-1,直线AF的方程为y=-x+2,
由$\left\{\begin{array}{l}{x=-2}\\{y=-x+2}\end{array}\right.$,可得A点坐标为(-2,4)
∵PA⊥l,A为垂足,
∴P点纵坐标为4,代入抛物线方程,得P点坐标为(2,4),
∴|PF|=|PA|=2-(-2)=4.
故选:B.
点评 本题主要考查抛物线的几何性质,定义的应用,以及曲线交点的求法,属于综合题.

练习册系列答案
相关题目
4.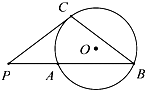 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
 如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )
如图,PC是⊙O的切线,C为切点,PAB为割线,PC=2,PA=1,∠P=60°,则BC=( )| A. | 3 | B. | 2 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
18.在△ABC中,a=3,b=5,c=7,那么这个三角形的最大角是( )
| A. | 135° | B. | 150° | C. | 90° | D. | 120° |
 如图,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.
如图,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=2$\sqrt{2}$,动点D在线段AB上.