题目内容
已知不等式ax2+bx+c>0的解集为(1,t),记函数f(x)=ax2+(a-b)x-c.
(1)求证:函数y=f(x)必有两个不同的零点;
(2)若函数y=f(x)的两个零点分别为m,n,求|m-n|的取值范围;
(3)是否存在这样的实数a,b,c及t使得函数y=f(x)在[-2,1]上的值域为[-6,12]?若存在,求出t的值及函数y=f(x)的解析式;若不存在,请说明理由.
(1)求证:函数y=f(x)必有两个不同的零点;
(2)若函数y=f(x)的两个零点分别为m,n,求|m-n|的取值范围;
(3)是否存在这样的实数a,b,c及t使得函数y=f(x)在[-2,1]上的值域为[-6,12]?若存在,求出t的值及函数y=f(x)的解析式;若不存在,请说明理由.
(1)见解析 (2)(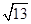 ,+∞) (3)f(x)=-2x2-8x+4.
,+∞) (3)f(x)=-2x2-8x+4.
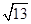 ,+∞) (3)f(x)=-2x2-8x+4.
,+∞) (3)f(x)=-2x2-8x+4.解:(1)证明:由题意知a+b+c=0,且-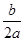 >1,a<0且
>1,a<0且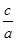 >1,
>1,
∴ac>0,
∴对于函数f(x)=ax2+(a-b)x-c有Δ=(a-b)2+4ac>0,
∴函数y=f(x)必有两个不同零点.
(2)|m-n|2=(m+n)2-4mn=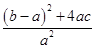 =
=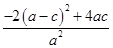 =(
=(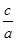 )2+8
)2+8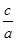 +4,
+4,
由不等式ax2+bx+c>0的解集为(1,t)可知,
方程ax2+bx+c=0的两个解分别为1和t(t>1),
由根与系数的关系知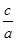 =t,
=t,
∴|m-n|2=t2+8t+4,t∈(1,+∞).
∴|m-n|>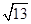 ,∴|m-n|的取值范围为(
,∴|m-n|的取值范围为(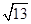 ,+∞).
,+∞).
(3)假设存在满足题意的实数a,b,c及t,
∵f(x)=ax2+(a-b)x-c=a[x2+(1-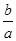 )x-
)x-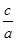 ]
]
=a[x2+(1+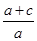 )x-
)x-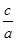 ]
]
=a[x2+(2+t)x-t](t>1),
∴f(x)的对称轴为x=-1- <-
<-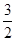 .
.
∴f(x)在[-2,1]上的最小值为f(1)=3a=-6,则a=-2.
要使函数y=f(x)在[-2,1]上的值域为[-6,12],
只要f(x)max=12即可.
①若-1- ≤-2,即t≥2,f(x)max=f(-2)=12,则有6t=12,
≤-2,即t≥2,f(x)max=f(-2)=12,则有6t=12,
∴t=2.
此时,a=-2,b=6,c=-4,t=2,∴f(x)=-2x2-8x+4.
②若-1- >-2,∴1<t<2,f(x)max=f(-1-
>-2,∴1<t<2,f(x)max=f(-1- )=
)=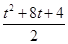 =12.
=12.
∴t=2或t=-10,舍去.
综上所述,当a=-2,b=6,c=-4,t=2时,函数y=f(x)在[-2,1]上的值域为[-6,12],此时函数的解析式为f(x)=-2x2-8x+4.
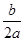 >1,a<0且
>1,a<0且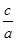 >1,
>1,∴ac>0,
∴对于函数f(x)=ax2+(a-b)x-c有Δ=(a-b)2+4ac>0,
∴函数y=f(x)必有两个不同零点.
(2)|m-n|2=(m+n)2-4mn=
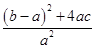 =
=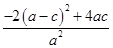 =(
=(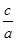 )2+8
)2+8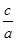 +4,
+4,由不等式ax2+bx+c>0的解集为(1,t)可知,
方程ax2+bx+c=0的两个解分别为1和t(t>1),
由根与系数的关系知
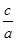 =t,
=t,∴|m-n|2=t2+8t+4,t∈(1,+∞).
∴|m-n|>
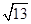 ,∴|m-n|的取值范围为(
,∴|m-n|的取值范围为(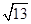 ,+∞).
,+∞).(3)假设存在满足题意的实数a,b,c及t,
∵f(x)=ax2+(a-b)x-c=a[x2+(1-
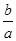 )x-
)x-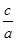 ]
]=a[x2+(1+
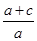 )x-
)x-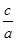 ]
]=a[x2+(2+t)x-t](t>1),
∴f(x)的对称轴为x=-1-
 <-
<-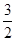 .
.∴f(x)在[-2,1]上的最小值为f(1)=3a=-6,则a=-2.
要使函数y=f(x)在[-2,1]上的值域为[-6,12],
只要f(x)max=12即可.
①若-1-
 ≤-2,即t≥2,f(x)max=f(-2)=12,则有6t=12,
≤-2,即t≥2,f(x)max=f(-2)=12,则有6t=12,∴t=2.
此时,a=-2,b=6,c=-4,t=2,∴f(x)=-2x2-8x+4.
②若-1-
 >-2,∴1<t<2,f(x)max=f(-1-
>-2,∴1<t<2,f(x)max=f(-1- )=
)=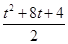 =12.
=12.∴t=2或t=-10,舍去.
综上所述,当a=-2,b=6,c=-4,t=2时,函数y=f(x)在[-2,1]上的值域为[-6,12],此时函数的解析式为f(x)=-2x2-8x+4.

练习册系列答案
相关题目
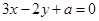 的两侧,则
的两侧,则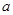 的取值范围是( )
的取值范围是( )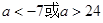
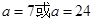
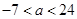
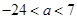
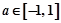 ,函数
,函数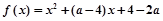 的值恒大于0,则x的范围是( )
的值恒大于0,则x的范围是( )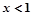 或
或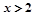

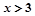
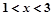
 x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.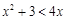 的解集为__________.
的解集为__________.