题目内容
设f(x)= x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
 x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.-3<t<3
∵ x2-bx+c<0的解集是(-1,3),
x2-bx+c<0的解集是(-1,3),
∴ >0且-1,3是
>0且-1,3是 x2-bx+c=0的两根,
x2-bx+c=0的两根,
∴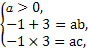 得
得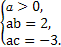
∵函数f(x)= x2-bx+c图象的对称轴方程为x=
x2-bx+c图象的对称轴方程为x= =1,且f(x)在[1,+∞)上是增函数,
=1,且f(x)在[1,+∞)上是增函数,
又∵7+|t|≥7>1,1+t2≥1,
则由f(7+|t|)>f(1+t2),得7+|t|>1+t2,
即|t|2-|t|-6<0,亦即(|t|+2)(|t|-3)<0,
∴|t|<3,即-3<t<3.
 x2-bx+c<0的解集是(-1,3),
x2-bx+c<0的解集是(-1,3),∴
 >0且-1,3是
>0且-1,3是 x2-bx+c=0的两根,
x2-bx+c=0的两根,∴
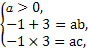 得
得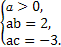
∵函数f(x)=
 x2-bx+c图象的对称轴方程为x=
x2-bx+c图象的对称轴方程为x= =1,且f(x)在[1,+∞)上是增函数,
=1,且f(x)在[1,+∞)上是增函数,又∵7+|t|≥7>1,1+t2≥1,
则由f(7+|t|)>f(1+t2),得7+|t|>1+t2,
即|t|2-|t|-6<0,亦即(|t|+2)(|t|-3)<0,
∴|t|<3,即-3<t<3.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 的不等式
的不等式 的解集为
的解集为 ,则关于
,则关于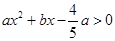 的解集为 .
的解集为 .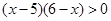 的解集是( )
的解集是( )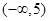
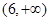
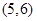
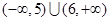
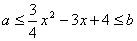 的解集为
的解集为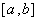 ,则
,则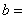 ,且
,且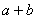 的值为 .
的值为 .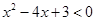 ;②
;②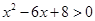 ;③
;③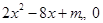 ﹒要使同时满足①式和②的所有
﹒要使同时满足①式和②的所有 的值都满足③式,则实数
的值都满足③式,则实数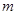 的取值范围是( )
的取值范围是( )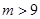 B.
B.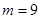 C﹒
C﹒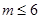 D﹒
D﹒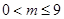

 若
若 ,则实数m的取值范围是( )
,则实数m的取值范围是( )