题目内容
设M是由满足下列两个条件的函数 构成的集合:
构成的集合:
①议程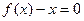 有实根;②函数
有实根;②函数 的导数
的导数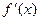 满足0<
满足0<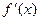 <1.
<1.
(I)若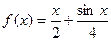 ,判断方程
,判断方程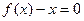 的根的个数;
的根的个数;
(II)判断(I)中的函数 是否为集合M的元素;
是否为集合M的元素;
(III)对于M中的任意函数 ,设x1是方程
,设x1是方程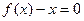 的实根,求证:对于
的实根,求证:对于 定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有
定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有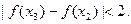
 构成的集合:
构成的集合:①议程
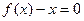 有实根;②函数
有实根;②函数 的导数
的导数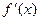 满足0<
满足0<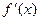 <1.
<1.(I)若
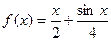 ,判断方程
,判断方程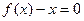 的根的个数;
的根的个数;(II)判断(I)中的函数
 是否为集合M的元素;
是否为集合M的元素;(III)对于M中的任意函数
 ,设x1是方程
,设x1是方程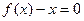 的实根,求证:对于
的实根,求证:对于 定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有
定义域中任意的x2,x3,当| x2-x1|<1,且| x3-x1|<1时,有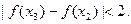
(1)唯一 (2)是
(I)令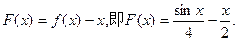
则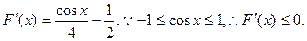
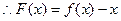 是单调递减函数.
是单调递减函数.
又取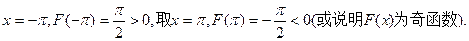
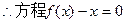 在其定义域上有唯一实根.
在其定义域上有唯一实根.
(II)由(I)知方程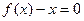 有实根(或者由
有实根(或者由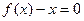 ,易知x=0就是方程的一个根),
,易知x=0就是方程的一个根), 满足条件①.
满足条件①.

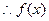 满足条件②.故
满足条件②.故 是集合M中的元素.
是集合M中的元素.
(III)不妨设 在其定义域上是增函数.
在其定义域上是增函数.
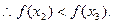
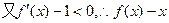 是其定义域上的减函数.
是其定义域上的减函数.
 .
.

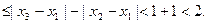
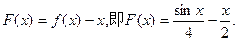
则
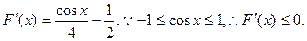
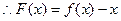 是单调递减函数.
是单调递减函数.又取
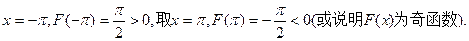
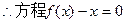 在其定义域上有唯一实根.
在其定义域上有唯一实根.(II)由(I)知方程
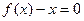 有实根(或者由
有实根(或者由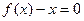 ,易知x=0就是方程的一个根),
,易知x=0就是方程的一个根), 满足条件①.
满足条件①.
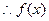 满足条件②.故
满足条件②.故 是集合M中的元素.
是集合M中的元素.(III)不妨设
 在其定义域上是增函数.
在其定义域上是增函数.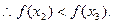
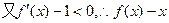 是其定义域上的减函数.
是其定义域上的减函数. .
.
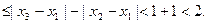

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
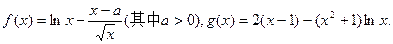
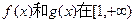 上单调性一致,求a的取值范围;
上单调性一致,求a的取值范围;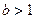 ,证明不等式
,证明不等式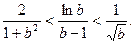
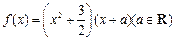 .
.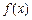 的图象上有与
的图象上有与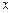 轴平行的切线,求
轴平行的切线,求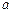 的范围;
的范围;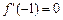 ,(Ⅰ)求函数
,(Ⅰ)求函数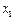 ,
,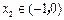 ,不等式
,不等式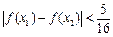 恒成立.
恒成立.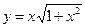 ;
;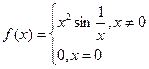 的导数
的导数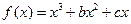 在
在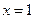 处取得极小值–2.(I)求
处取得极小值–2.(I)求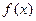 的单调区间;(II)若对任意的
的单调区间;(II)若对任意的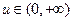 ,函数
,函数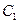 与函数
与函数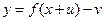 的图像
的图像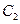 至多有一个交点.求实数
至多有一个交点.求实数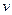 的范围.
的范围.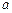 为实数,
为实数,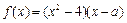 ,
,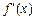 ;
;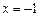 是函数
是函数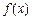 的极值点,求
的极值点,求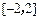 上的最大值和最小值;
上的最大值和最小值;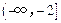 和
和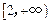 上都是递增的,求
上都是递增的,求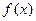
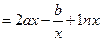
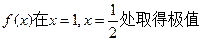 ,
, 

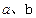 的值;
的值;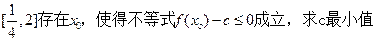
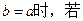
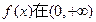 上是单调函数,求
上是单调函数,求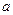 的取值范围。
的取值范围。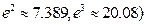
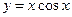 在
在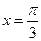 处的导数值是___________.
处的导数值是___________.