题目内容
【题目】下列命题中是假命题的是( )
A.?![]() ∈R,使sin(
∈R,使sin(![]() )=
)=![]() +sinβ
+sinβ
B.?![]() ∈R,函数f(x)=sin(
∈R,函数f(x)=sin(![]() )都不是偶函数
)都不是偶函数
C.?m∈R,使f(x)=(m-1)·m2-4m+3是幂函数,且在(0,+∞)上单调递减
D.?![]() >0,函数f(x)=ln2x+lnx-
>0,函数f(x)=ln2x+lnx-![]() 有零点
有零点
【答案】B
【解析】对于A,当α=0时,sin(α+β)=sinα+sinβ成立;对于B,当φ=![]() 时,f(x)=sin(2x+φ)=cos2x为偶函数;对于C,当m=2时,f(x)=(m-1)·xm2-4m+3=x-1=
时,f(x)=sin(2x+φ)=cos2x为偶函数;对于C,当m=2时,f(x)=(m-1)·xm2-4m+3=x-1=![]() , 满足条件;对于D,令lnx=t , a>0,对于方程t2+t-a=0,Δ=1-4(-a)>0,方程恒有解,故满足条件.综上可知,故选B.
, 满足条件;对于D,令lnx=t , a>0,对于方程t2+t-a=0,Δ=1-4(-a)>0,方程恒有解,故满足条件.综上可知,故选B.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.

练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: 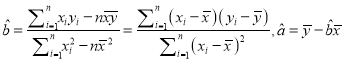 .
.