Question

【题目】如图，四棱锥P－ABCD中，底面ABCD为梯形，PD⊥底面ABCD，AB∥CD，AD⊥CD，AD＝AB＝1，BC＝.

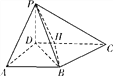
(Ⅰ)求证：平面PBD⊥平面PBC；

(Ⅱ)设H为CD上一点，满足＝2，若直线PC与平面PBD所成的角的正切值为，求二面角H－PB－C的余弦值．

Answer 1

【答案】(Ⅰ)见解析；(Ⅱ) .

【解析】试题分析：（Ⅰ）通过勾股定理可得BC⊥BD，利用面面垂直的判定定理即得结论；
（Ⅱ）通过题意以D为原点，DA、DC、DP分别为x、y、z轴建立坐标系，所求二面角的余弦值即为平面HPB的一个法向量与平面PBC的一个法向量的夹角的余弦值，计算即可．

试题解析：

(Ⅰ)证明：由AD⊥CD，AB∥CD，AD＝AB＝1BD＝，

又BC＝，∴CD＝2，∴BC⊥BD，因为PD⊥底面ABCD，∴BC⊥PD.

因为PD∩BD＝D，所以BC⊥平面PBD，所以平面PBD⊥平面PBC.

(Ⅱ)由(Ⅰ)可知∠BPC为PC与底面PBD所成的角．

所以tan∠BPC＝，

所以PB＝，PD＝1，又＝2及CD＝2，

可得CH＝，DH＝.

以D点为坐标原点，DA，DC，DP分别x，y，z轴建立空间坐标系，则B(1，1，0)，P(0，0，1)，C(0，2，0)，H.

设平面HPB的法向量为n＝(x1，y1，z1)，

则由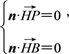得取n＝(1，－3，－2)，

设平面PBC的法向量为m＝(x2，y2，z2)，

则由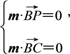得取m＝(1，1，2)．

所以cos〈m·n〉＝＝－，所以二面角H－PB－C余弦值为.