Question

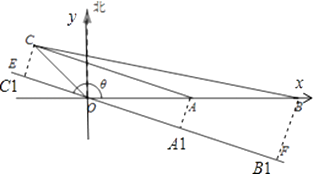
【题目】如图，O为总信号源点，A，B，C是三个居民区，已知A，B都在O的正东方向上，OA=10km，OB=20km，C在O的北偏西45°方向上，CO=5 km．
（1）求居民区A与C的距离；
（2）现要经过点O铺设一条总光缆直线EF（E在直线OA的上方），并从A，B，C分别铺设三条最短分光缆连接到总光缆EF．假设铺设每条分光缆的费用与其长度的平方成正比，比例系数为m（m为常数）．设∠AOE=θ（0≤θ＜π），铺设三条分光缆的总费用为w（元）． ①求w关于θ的函数表达式；
②求w的最小值及此时tanθ的值．

Answer 1

【答案】
（1）解：以点O位坐标原点，OA为x轴建立直角坐标系，则A（10，0），B（20，0），C（﹣5，5），

∴AC= =5 ；

（2）解：①当直线l的斜率存在时，设l：y=kx，k=tanθ，

则w=m[ + + ]=m ；

直线l的斜率不存在时，w=m（100+400+25）=525m，

综上，w=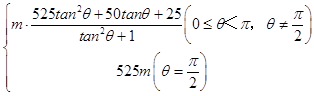

②直线l的斜率不存在时，w=m（100+400+25）=525m；

当直线l的斜率存在时，w=m

令t=k﹣10，则t=0时，w=525m；

t≠0时，w=525m+m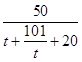

∵t+ ≤﹣2 ，或t+ ≥2 ，

∴w的最小值为525m+m =（275﹣25 ）m，

此时，t=﹣ ，tanθ=k=10﹣ ．

【解析】（1）以点O位坐标原点，OA为x轴建立直角坐标系，求出A，C的坐标，即可求居民区A与C的距离；（2）①分类讨论，求出铺设三条分光缆的总费用，即可求w关于θ的函数表达式；②换元，利用基本不等式，可求w的最小值及此时tanθ的值．