Question

【题目】在直角坐标系xOy中，圆C的参数方程 为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求圆C的极坐标方程；
（2）直线l的极坐标方程是 ，射线 与圆C的交点为O，P，与直线l的交点为Q，求|OP||OQ|的范围．

Answer 1

【答案】
（1）解：∵圆C的参数方程 为参数），

∴消去参数φ，得圆C的普通方程是（x﹣1）2+y2=1，

又x=ρcosθ，y=ρsinθ，

∴圆C的极坐标方程是ρ=2cosθ．

（2）解：设P（ρ1，θ1），则有ρ1=2cosθ1，Q（ρ2，θ1），

则有 ，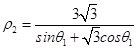

∴ ，

∵tanθ1＞0，∴0＜|OP||OQ|＜6．

故|OP||OQ|的范围是（0，6）．

【解析】（1）圆C的参数方程消去参数φ，能求出圆C的普通方程，再由x=ρcosθ，y=ρsinθ，能求出圆C的极坐标方程．（2）设P（ρ1，θ1），则有ρ1=cosθ1，Q（ρ2，θ1），则 ，|OP||OQ|=ρ1ρ2，结合tanθ1＞0，能求出|OP||OQ|的范围．