题目内容
【题目】已知f(x)是定义在R上的偶函数,且f(x+2)=f(x)对x∈R恒成立,当x∈[0,1]时,f(x)=2x , 则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.1
【答案】B
【解析】解:∵f(x+2)=f(x)对x∈R恒成立,
∴f(x)的周期为2,(x)是定义在R上的偶函数,
∴ ![]() =f(﹣
=f(﹣ ![]() )=f(
)=f( ![]() )
)
∵当x∈[0,1]时,f(x)=2x,
∴f( ![]() )=
)= ![]() ,
,
故选:B.
【考点精析】认真审题,首先需要了解函数奇偶性的性质(在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇).

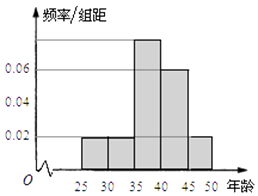
【题目】某单位280名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第1,2,3组的员工人数分别是多少?
(II)为了交流读书心得,现从上述12人中再随机抽取3人发言,设3人中年龄在[35,40)的人数为ξ,求ξ的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附: ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |