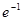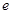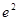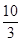题目内容
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],
都有|f(x)-g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“紧密函数”.若
 与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( )
与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( )
都有|f(x)-g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“紧密函数”.若
 与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( )
与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( )| A.[0,1] | B.[2,3] | C.[1,2] | D.[1,3] |
A
因为f(x)与g(x)在[a,b]上是“紧密函数”,则|f(x)-g(x)|≤1即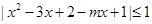 在[1,2]上成立,即|
在[1,2]上成立,即|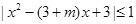 在[1,2]上成立,化简得
在[1,2]上成立,化简得
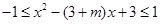 在[1,2]上成立,∴
在[1,2]上成立,∴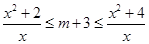
即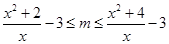 在x∈[1,2]上成立.
在x∈[1,2]上成立.
令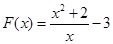 ,,x∈[1,2],则
,,x∈[1,2],则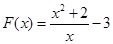 在
在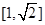 上单调递减,在
上单调递减,在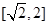 上单调递增,所以F(x)的最大值为F(2)="0;"
上单调递增,所以F(x)的最大值为F(2)="0;" 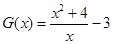 在[1,2]上是减函数,所以G(x)的最小值为G(2)=1.∴0≤m≤1.
在[1,2]上是减函数,所以G(x)的最小值为G(2)=1.∴0≤m≤1.
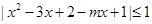 在[1,2]上成立,即|
在[1,2]上成立,即|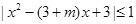 在[1,2]上成立,化简得
在[1,2]上成立,化简得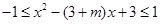 在[1,2]上成立,∴
在[1,2]上成立,∴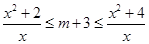
即
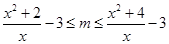 在x∈[1,2]上成立.
在x∈[1,2]上成立.令
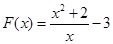 ,,x∈[1,2],则
,,x∈[1,2],则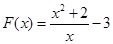 在
在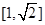 上单调递减,在
上单调递减,在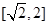 上单调递增,所以F(x)的最大值为F(2)="0;"
上单调递增,所以F(x)的最大值为F(2)="0;" 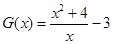 在[1,2]上是减函数,所以G(x)的最小值为G(2)=1.∴0≤m≤1.
在[1,2]上是减函数,所以G(x)的最小值为G(2)=1.∴0≤m≤1.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的函数
上的函数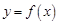 是偶函数,且
是偶函数,且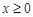 时,
时, 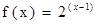 .
.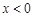 时,求
时,求 解析式;
解析式; ,求
,求 取值的集合.
取值的集合.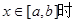 ,函数的值域为
,函数的值域为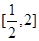 ,求
,求 满足的条件。
满足的条件。
 的单调区间;
的单调区间;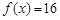 ,求相应的值。
,求相应的值。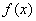 是定义在
是定义在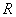 上的偶函数,在
上的偶函数,在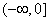 上是增函数,则使得
上是增函数,则使得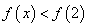 的
的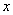 取值范围是( )
取值范围是( )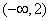
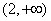
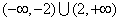
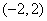
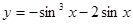 的最小值是__________。
的最小值是__________。 是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。
是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。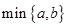 表示
表示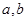 两数中的最小值,若函数
两数中的最小值,若函数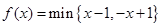 ,则不等式
,则不等式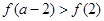 的解集是________________.
的解集是________________.  的最大值为( )
的最大值为( )