题目内容
(12分)设 是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。
是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。
 是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。
是奇函数,(a,b,c∈Z),且f(1)=2,f(2)<3,求a,b,c的值。a=b=1,c=0
因为函数为奇函数,那么利用奇函数的性质得到参数c=0,又f(1)=2,得a+1=2b,而f(2)<3得到a的范围,进而得打参数a,b的值。
解:由f(-x)=-f(x)得-bx+c="-(bx+c)," ∴c=0 …….. 4分
又f(1)=2,得a+1=2b,而f(2)<3,得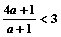
解得-1<a<2,又a∈Z, ∴a=0或a=1
当a=0时,b=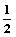 (舍),当a=1时,b=1
(舍),当a=1时,b=1
∴a=b=1,c=0…………………………………………12分
解:由f(-x)=-f(x)得-bx+c="-(bx+c)," ∴c=0 …….. 4分
又f(1)=2,得a+1=2b,而f(2)<3,得
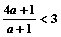
解得-1<a<2,又a∈Z, ∴a=0或a=1
当a=0时,b=
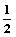 (舍),当a=1时,b=1
(舍),当a=1时,b=1∴a=b=1,c=0…………………………………………12分

练习册系列答案
相关题目
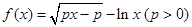 .
. 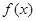 在定义域内为增函数,求实数
在定义域内为增函数,求实数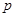 的取值范围;
的取值范围;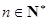 时,试判断
时,试判断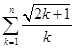 与
与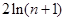 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;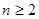 且
且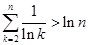 .
.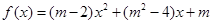 是偶函数,
是偶函数,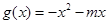 在
在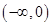 内单调递增,则实数
内单调递增,则实数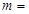 ( )
( )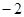
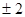
 ,其中
,其中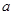 、
、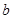 为常数,
为常数,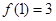 ,则
,则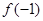 =_____________.
=_____________.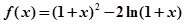 .
.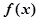 的单调区间;
的单调区间;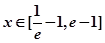 时,(其中
时,(其中 不等式
不等式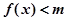 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;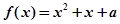 在区间[0,2]上的根的个数.
在区间[0,2]上的根的个数. 的单调增区间是______________.
的单调增区间是______________.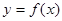 是定义在区间
是定义在区间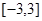 上的奇函数,且在
上的奇函数,且在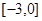 上单调递增,若
上单调递增,若 满足:
满足: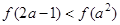 ,求
,求 与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( )
与g(x)=mx-1在[1,2]上是“紧密函数”,则m的取值范围是( ) 在实数集上是减函数,若
在实数集上是减函数,若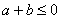 ,则下列正确的是 ( )
,则下列正确的是 ( )