题目内容
【题目】在直角坐标系xoy中，直l线l的参数方程为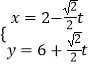 
（t为参数）．在极坐标系（与直角坐标系xoy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为ρ=10cosθ．
（1）求圆C的直角坐标方程；
（2）设圆C与直线l交于点A、B，若点P的坐标为（2，6），求|PA|+|PB|．
【答案】
（1）解：由ρ=10cosθ得ρ2=10ρcosθ，
∴直角坐标方程为：x2+y2=10x，配方为：（x﹣5）2+y2=25
（2）解：将l的参数方程代入圆C的直角坐标方程，化为 
=0，
由于△= 
﹣4×20=82＞0，可设t1，t2是上述方程的两个实根．
∴t1+t2=﹣ 
，t1t2=20，又直线l过点P（2，6），
可得：|PA|+|PB|=|t1|+|t2|=﹣（t1+t2）=9 
【解析】（1）由ρ=10cosθ得ρ2=10ρcosθ，把 
代入即可得出．（2）将l的参数方程代入圆C的直角坐标方程，化为 
=0，可设t1，t2是上述方程的两个实根．利用|PA|+|PB|=|t1|+|t2|=﹣（t1+t2）即可得出．
练习册系列答案
相关题目
【题目】在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q1为0.25，在B处的命中率为q2 ， 该同学选择先在A处投一球，以后都在B处投，用ξ表示该同学投篮训练结束后所得的总分，其分布列为：
ξ | 0 | 2 | 3 | 4 | 5 |
p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
（1）求q2的值；
（2）求随机变量ξ的数学期望Eξ；
（3）试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小．
